Kvadrat tənliklər ☰

Kvadrat tənliyin ümumi forması:
\(ax^2+bx+c=0\)
Burada \(a≠0\), \(a\), \(b\) və \(c\) verilmiş ədədlər (konstant), \(x\) isə məchuldur. \(a\) birinci əmsal (və ya baş əmsal), \(b\) – ikinci əmsal, \(c\) – sərbəst hədd adlanır. Kvadrat tənliyi kvadrat düsturdan istifadə etməklə həll etmək olar:
\(x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{{2a}}\)
Kvadrat düstur diskriminantdan \((b^2–4ac)\) asılı olaraq, real və ya kompleks həllər təmin edir. Diskriminant müsbət olarsa, kvadrat tənliyin iki fərqli həqiqi kökü var. Diskriminant sıfırdırsa, kvadrat tənliyin bir həqiqi kökü var (iki bərabər kök). Diskriminant mənfi olarsa, kvadrat tənliyin iki kompleks kökü olur.

Natamam kvadrat tənliklər:

\(ax^2+bx+c=0\) kvadrat tənliyində \(b\) və \(c\) əmsallarının heç olmasa biri sıfıra bərabər olarsa, belə tənliyə natamam kvadrat tənlik deyilir.

Kvadrat tənliklərin həlli. ☰

Kvadrat tənliklərin həlli üçün bir neçə üsul var, o cümlədən:

• Vuruqlara ayırma üsulu: Bu, kvadrat ifadəni iki binomun hasili kimi yazmağı və tənliyin köklərini tapmaq üçün hər binomialı sıfıra bərabər təyin etməyi əhatə edir.
• Tam kvadrat ayırmaqla: Bu, kvadrat ifadəni mükəmməl kvadrat trinomial formaya çevirməyi və sonra əsas cəbrdən istifadə edərək kökləri həll etməyi əhatə edir.
• Kvadrat tənliyin kökləri düsturu: Bu düstur istənilən kvadrat tənliyin köklərini onun əmsalları baxımından verir və tam kvadrat ayırmaq üsulundan istifadə etməklə əldə edilə bilər.
• Qrafik üsul: Bu, kvadrat funksiyanın qrafikini qurmağı və tənliyin köklərinə uyğun gələn \(x\)-kəsiciləri müəyyən etməyi əhatə edir.

Bu metodların hər birinin öz üstünlükləri və mənfi cəhətləri var. Metodun seçimi konkret problemdən, mövcud vasitələrdən və resurslardan asılıdır.


Vuruqlara ayırma üsulu:
Vuruqlara ayırma üsulu kvadratik ifadələri vuruqlara ayırmaq və kvadrat tənlikləri həll etmək üçün istifadə olunan bir texnikadır. Bu üsuldan istifadə edərək kvadrat ifadəni vuruqlara ayırmaq üçün bir-birinə vurulduqda eyni kvadrat tənliyi verən iki binom tapmalıyıq. Kvadrat ifadənin ümumi forması belədir:
\(ax^2+bx+c\)

Vuruqlara ayırmaq üçün, \((mx+r)(nx+s)\) düsturundan istifadə edə bilərik. Burada \(m, n, r\) və \(s\) sabitlərdir. Bu iki binomun hasilindən \(mnx^2+(ms+rn)x+rs\) alırıq. Bunu kvadrat ifadənin ümumi forması ilə müqayisə etsək görərik ki:
\(mn=a\)
\(ms+rn=b\)
\(rs=c\)

Bunları istifadə edərək \(m, n, r\) və \(s\) -i tapa bilərik. Bu sabitləri tapdıqdan sonra kvadrat ifadəni
\(ax^2+bx+c=(mx+r)(nx+s) \) formasında yaza bilərik.
Yuxarıda göstərildiyi kimi vuruqlara ayırdıqdan sonra \(0\)-a vurma xüsusiyyətindən istifadə edərək tənliyin köklərini tapa bilərik. Bu o deməkdir ki, hasilin 0-a bərabər olması üçün vuruqlardan ən azı biri 0-a bərabər olmalıdır.
Buna görə də, kvadratik ifadəni \((mx+r)(nx+s)=0\) kimi vuruqlara ayırmışıqsa, onda hər bir əmsalı sıfıra bərabər edib \(x\) -i tapa bilərik:
\((mx+r)=0 \) və ya \((nx+s) =0\)
Bu tənlikləri həll etdikdə, alırıq:
\(x=-\frac{r}{m}\) və ya \(x=-\frac{s}{n}\)
Bu o deməkdir ki, kvadrat tənliyin kökləri \(x=-\frac{r}{m}\) və ya \(x=-\frac{s}{n}\)-dir.
Qeyd etmək lazımdır ki, bütün kvadrat ifadələri həqiqi ədədlərdən istifadə etməklə vuruqlara ayırmaq olmaz. Belə hallarda tənliyin köklərini tapmaq üçün başqa üsullardan istifadə etməmiz lazım ola bilər.

Misallar:
\(x^2-5x+6=0\) tənliyini həll edin.
Bu tənliyi vuruqlara ayırma üsulu ilə həll etməyə çalışaq.
Bunun üçün \((mx+r)(nx+s)\) formasından istifadə edək. \(m, n, r\) və \(s\) sabitlərdir.
Bildiyimiz kimi, bu iki binomun hasili bizə \(mnx^2+(ms+rn)x+rs\) verir.
Deməli \(x^2–5x+6\) tənliyi üçün alırıq:
\(mn=1 \)
\(ms+rn=-5 \)
\(rs=6 \)
\(m, n, r\) və \(s\)-ə uyğun gələ biləcək müxtəlif dəyərləri tapıb yoxlayırıq. İndiki halda \(m=1, n=1, r=-2\) və \(s=-3\) alaraq sabitləri uyğun yerlərə yazaq:
\((mx+r)(nx+s) \)
\((x-2)(x-3)=0 \)
Bu halda kvadrat tənliyin köklərinin \(x=2\) və \(x=3\) olduğunu görürük.
\(x^2-5x+6=0\) kvadrat tənliyində aldığımız kökləri yazaraq cavabların doğruluğunu yoxlayaq.
\(2^2-5\cdot 2+6=0 \)
\(3^2-5\cdot 3+6=0 \)
Bərabərlik doğrudur. Deməli \(x=2\) və \(x=3\) tənliyin kökləridir.


Tam kvadrat ayırmaqla:
Əvvəlcə kvadrat ifadəni tam kvadrat şəklində yazmalıyıq.
Tam kvadrat \((x+a)^2=x^2+2ax+a^2\) formasının ifadəsidir, burada \(a\) sabitdir. İstənilən kvadrat ifadə sabiti toplamaq və ya çıxmaqla tam kvadrat şəklində yazıla bilər.
\(ax^2+bx+c=0\) kvadrat tənliyimiz olduğunu hesab edək.
İlk öncə kvadrat tənliyin kökləri düsturunu alaq.

\(a(x^2 + \frac{b}{a}x) = -c\)

\(a\left(x^2 + \frac{b}{a}x + \frac{b^2}{4a^2}\right) = -c + a(\frac{b^2}{4a^2})\)

\(a\left(x + \frac{b}{2a}\right)^2 = \frac{4ac - b^2}{4a}\)

Hər iki tərəfi \(a\) -ya bölərək alırıq:

\((x + \frac{b}{2a})^2 = \frac{4ac - b^2}{4a^2}\)

\(x + \frac{b}{2a} = \sqrt{\frac{4ac - b^2}{4a^2}}\)

\(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)

Bu düstur \(ax^2+bx+c=0\) formasında olan istənilən kvadrat tənliyin köklərini almağa imkan verir.
Burada \(b^2–4ac\) diskriminant adlanır. Əgər diskriminant mükəmməl kvadratdırsa deməli kvadrat tənlik tam kvadrat şəklində yazıla bilər.

Misallar:
\(x^2+6x+1=0\) kvadrat tənliyini nəzərdən keçirək.
Kvadrata tamamlamaq üçün bu tənliyi \((x+a)^2+b\) formasında yazmalıyıq. Burada \(a\) və \(b\) sabitlərdir.
İlk öncə tənliyin sol tərəfinə \((\frac{b}{2})^2\) yəni, \((\frac{6}{2})^2 =9\) əlavə edib çıxmalıyıq.
\(x^2+6x+9-9+1=0\) tənliyini alırıq. Diqqət etdikdə görürük ki, sol tərəfdəki ilk 3 hədd \((x+3)^2\) formasında yazıla biləcək mükəmməl kvadrat trinomial əmələ gətirir.
Bu halda biz bu tənliyi \((x+3)^2-8=0\) formasında yaza bilərik.
İndi bu tənliyi həll edək.
\((x+3)^2=8 \)
\(x+3=\pm \sqrt{8} \)
\(x=-3 \pm \sqrt{8} \)
Tənliyin kökləri:
\(x=-3+ \sqrt{8} \) və \(x=-3- \sqrt{8} \)


Qrafik üsul:
Qrafik, kvadrat tənliklərin həlli üçün vizual bir üsuldur. Bu metodun arxasında duran ideya kvadrat tənliyin qrafikini çəkmək və tənliyin həllərinə uyğun gələn \(x\)-kəsiciləri müəyyən etməkdir. Kvadrat tənliyin qrafikini çəkmək üçün əvvəlcə onu \(y=ax^2+bx+c\) şəklində yenidən yazırıq, burada \(y\) asılı dəyişən, \(x\) isə müstəqil dəyişəndir. Kvadrat tənliyin qrafiki U formalı əyri olan paraboladır. Parabolanın istiqaməti və forması \(a\) əmsalının işarəsindən asılıdır. Əgər \(a > 0\) olarsa, parabola yuxarıya, \(a < 0\) olarsa, aşağıya doğru açılır.
Parabolanın \(x\)-kəsicilərini tapmaq üçün \(y=0\) təyin edirik və \(x\) üçün həll edirik. Bu, parabolanın \(x\) oxunu kəsdiyi yerdə \(x\)-in qiymətlərini verir. Bu qiymətlər kvadrat tənliyin həllərinə uyğundur.
Bu üsula bir nümunə üzərində baxaq.
\(x^2-4x-5=0\) tənliyini həll edək.
Tənliyi \(y=x^2–4x-5\) şəklində yazaq. Qrafiki çəkmək üçün müxtəlif qrafik kalkulyatorlardan, proqramlardan istifadə edə və ya əl ilə çəkə bilərik.

Qrafik:


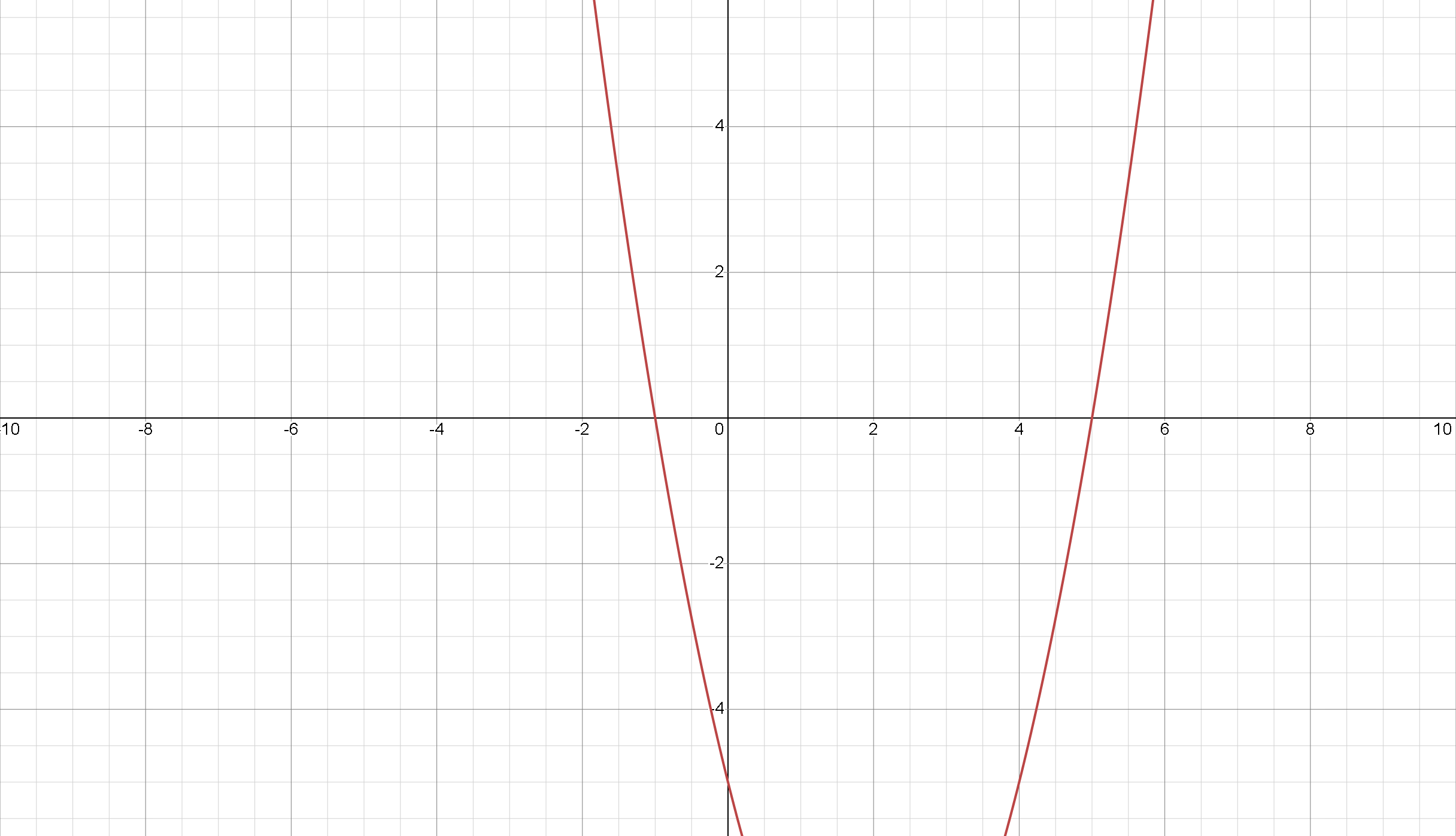
Parabolanın \(x\) oxunu tənliyin həllərinə uyğun gələn iki nöqtədə kəsdiyini görə bilərik. Bu nöqtələri tapmaq üçün ya kvadrat düsturdan istifadə edə bilərik, ya da qrafikdən \(x\)-in qiymətlərini təxmin edə bilərik. Bu halda \(x\)-kəsicilər kvadrat tənliyin həlli olan təqribən \(x=-1\) və \(x=5\) olur.
Xülasə, qrafik üsul kvadrat tənliklərin vizual həlli üçün faydalı bir üsuldur. Tənliyin qrafikini çəkmək və \(x\)-kəsiciləri müəyyən etməklə biz tənliyin həll yollarını tez tapa bilərik.

Kvadrat tənliyin kökləri düsturu ☰

\(ax^2+bx+c=0\) formasında tənlik üçün

\(x =\frac{-b \pm \sqrt{b^2- 4ac}}{2a}\)

kvadrat tənliyin kökləri düsturu adlanır.
Bu düstur bizə kvadrat tənliyin kökləri və ya həlləri olan \(x\)-i verir. \(\pm\) simvolu həm müsbət, həm də mənfi kökləri tapmaq lazım olduğunu bildirir. Kvadrat kökün içindəki ifadə \((b^2– 4ac)\) kvadrat tənliyin diskriminantı adlanır və bu, tənliyin neçə real kökə malik olduğunu bildirir.

Əgər diskriminant müsbətdirsə \((b^2–4ac>0)\), kvadrat tənliyin yuxarıdakı düsturla verilmiş iki fərqli həqiqi kökü var.

Diskriminant sıfırdırsa \((b^2–4ac=0)\), kvadrat tənliyin bir həqiqi kökü var və bu, \(x=-\frac{b}{2a}\) ilə verilir.

Diskriminant mənfi olarsa \((b^2– 4ac < 0)\), kvadrat tənliyin iki mürəkkəb kökü var və bunlar aşağıdakı kimi verilir:

\(x =\frac{-b \pm i\sqrt{4ac-b^2}}{2a}\)

burada \(i\), \(-1\)-in kvadrat kökünə bərabər olan xəyali vahiddir. Kvadrat tənliyin kökləri düsturu kvadrat tənliklərin həlli üçün güclü vasitədir və \(a\), \(b\) və \(c\) əmsallarının qiymətlərindən asılı olmayaraq istənilən kvadrat tənlik üçün istifadə edilə bilər.

Viyet teoremi☰

Teorem: \(ax^2+bx+c=0\) kvadrat tənliyin köklərinin cəmi \(-\frac{b}{a}\)-ya, köklərinin hasili isə \(\frac{c}{a}\)-ya bərabərdir.
Yəni, \(ax^2+bx+c=0\) olduqda:
\(x_1+x_2=-\frac{b}{a}\), \(x_1\cdot x_2=\frac{c}{a}\) doğrudur.
İstənilən \(ax^2+bx+c=0\) kvadrat tənliyinin hər iki tərəfini \(a\)-ya bölməklə, onunla eynigüclü olan
\(x^2+\frac{b}{a} \cdot x+\frac{c}{a}=0\) çevrilmiş kvadrat tənliyini ala bilərik. Bu halda,
\(x_1+x_2=-b\) , \(x_1\cdot x_2=c\) doğrudur.

Tərs teorem: \(m\) və \(n\) ədədlərinin cəmi \(-p\)-yə hasili isə \(q\)-yə bərabərdirsə bu ədədlər \(x^2+px+q=0\) tənliyinin kökləridir.
Başqa sözlə, istənilən \(m\) və \(n\) ədədləri \(x^2-(m+n)x+m\cdot n=0\) tənliyinin kökləridir.

Misal: \(x^2+5x+6=0\) kvadrat tənliyi üçün viyet teoremini tətbiq edək.
\(x_1+x_2=-\frac{5}{1}=-5\) , \(x_1\cdot x_2=\frac{6}{1}=6\) olduqda, köklər \(-2\) və \(-3\)-ə uyğun gəlir.
\(-2+(-3)=-\frac{5}{1}\), \(-2\cdot (-3)=\frac{6}{1}\).