Квадратные уравнения ☰

Общая форма квадратного уравнения:
\(ax^2+bx+c=0\) , где \(a≠0\), \(a\), \(b\) и \(c\) - константы, а \(x\) - переменная.
Квадратное уравнение можно решить, используя квадратную формулу, которая выглядит так:
\(x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{{2a}}\)
Квадратная формула предоставляет решения для квадратного уравнения, которые могут быть действительными или комплексными, в зависимости от дискриминанта \((b^2–4ac)\). Если дискриминант положителен, у квадратного уравнения есть два различных действительных корня. Если дискриминант равен нулю, у квадратного уравнения есть один действительный корень, который является двойным корнем. Если дискриминант отрицателен, у квадратного уравнения есть два комплексных корня.

Неполные квадратные уравнения:

Если хотя бы один из коэффициентов \(b\) и \(c\) в квадратном уравнении \(ax^2+bx+c=0\) равен нулю, то уравнение называется неполным квадратным уравнением.

Решение квадратных уравнений ☰

Существует несколько методов решения квадратных уравнений, включая:

• Факторизация: Этот метод включает запись квадратного выражения в виде произведения двух биномов и приравнивание каждого бинома к нулю для нахождения корней уравнения.
• Дополнение квадрата: Этот метод включает преобразование квадратного выражения в форму полного квадрата трехчлена, а затем нахождение корней с помощью базовой алгебры.
• Квадратная формула: Эта формула дает корни любого квадратного уравнения в терминах его коэффициентов и может быть выведена с помощью метода дополнения квадрата.
• Графический метод: Этот метод включает построение графика квадратной функции и определение \(x\)-перехватов, которые соответствуют корням уравнения.
• Численные методы: Существует несколько численных методов, которые можно использовать для приближенного нахождения корней квадратного уравнения, такие как метод Ньютона, метод бисекции и метод секущих.

Каждый из этих методов имеет свои преимущества и недостатки, и выбор метода зависит от конкретной задачи и имеющихся инструментов и ресурсов.


Метод факторизации квадратных уравнений:
Метод факторизации - это техника, используемая для факторизации квадратных выражений и решения квадратных уравнений. Чтобы факторизовать квадратное выражение с использованием этого метода, нам нужно найти два бинома, которые умножаются друг на друга, чтобы получить квадратное выражение. Общая форма квадратного выражения:
\(ax^2+bx+c\)

Для факторизации этого квадратного выражения мы можем искать два бинома в виде:
\((mx+r)(nx+s)\) , где \(m\), \(n\), \(r\) и \(s\) - константы. Раскрыв произведение этих двух биномов, мы получаем:
\(mnx^2+(ms+rn)x+rs\).
Сравнив это с общей формой квадратного выражения, мы видим, что:
\(mn=a\)
\(ms+rn=b\)
\(rs=c\)

Мы можем использовать эти уравнения, чтобы найти \(m, n, r\) и \(s\). После того как мы найдем эти константы, мы можем записать квадратное выражение в виде фактора:
\(ax^2+bx+c=(mx+r)(nx+s) \).
Чтобы решить квадратное уравнение, используя метод факторизации, мы сначала факторизуем квадратное выражение, как показано выше. После того как мы разложили квадратное выражение, мы можем использовать свойство нулевого произведения, чтобы найти корни уравнения. Свойство нулевого произведения гласит, что если произведение двух множителей равно нулю, то хотя бы один из множителей должен быть равен нулю. Поэтому, если мы разложили квадратное выражение как:
\((mx+r)(nx+s)=0\), то мы можем приравнять каждый множитель нулю и решить для \(x\):
\((mx+r)=0 \) или \((nx+s) =0\)
Решая каждое линейное уравнение, мы получаем:
\(x=-\frac{r}{m}\) или \(x=-\frac{s}{n}\)
Следовательно, корни квадратного уравнения равны \(x=-\frac{r}{m}\) или \(x=-\frac{s}{n}\).
Следует отметить, что не все квадратные выражения можно факторизовать с использованием действительных чисел. В таких случаях нам может потребоваться использовать другие методы, такие как дополнение квадрата или квадратная формула, чтобы найти корни уравнения.

Пример:
Предположим, у нас есть квадратное уравнение: \(x^2-5x+6=0\).
Чтобы решить это уравнение с использованием метода факторизации, нам нужно разложить квадратное выражение \( x^2–5x+6 \) на произведение двух биномов. Мы можем искать два бинома в виде:
\((mx+r)(nx+s)\), где \(m\), \(n\), \(r\) и \(s\) - константы. Раскрыв произведение этих двух биномов, мы получаем:
\(mnx^2+(ms+rn)x+rs\).
Сравнив это с квадратным выражением \( x^2 –5x+6 \), мы видим, что:
\(mn=1 \)
\(ms+rn=-5 \)
\(rs=6 \)
Мы можем попробовать различные значения \(m\), \(n\), \(r\) и \(s\) до тех пор, пока не найдем значения, которые удовлетворяют этим уравнениям.
Одним из возможных наборов значений является \(m=1\), \(n=1\), \(r=-2\) и \(s=-3\), которые дают:
\((mx+r)(nx+s) \)
\((x-2)(x-3)=0 \)
Следовательно, корни квадратного уравнения равны \(x=2\) и \(x=3\)
Мы можем проверить, что эти значения действительно являются корнями квадратного уравнения, подставив их в исходное уравнение
\(2^2-5\cdot 2+6=0 \)
\(3^2-5\cdot 3+6=0 \)
Оба этих уравнения верны, поэтому \(x=2\) и \(x=3\) действительно являются корнями квадратного уравнения.


Дополнение квадрата:
Сначала нам нужно записать квадратное выражение в форме полного квадрата. Полным квадратом является выражение вида \( (x+a)^2=x^2+2ax+a^2\) , где \(a\) - постоянная. Любое квадратное выражение можно записать в виде полного квадрата, добавив или вычитая константу.
Предположим, у нас есть квадратное уравнение вида: \(ax^2+bx+c=0\)
Чтобы решить это уравнение, разделим его на полный квадрат, сначала записав квадратное выражение как полный квадрат, добавив или вычитая константу. Мы можем сделать это, дополнив квадрат, следующим образом:

\( a(x^2 + \frac{b}{a}x) = -c \)

\(a\left(x^2 + \frac{b}{a}x + \frac{b^2}{4a^2}\right) = -c + a(\frac{b^2}{4a^2})\)

\(a\left(x + \frac{b}{2a}\right)^2 = \frac{4ac - b^2}{4a}\)

Теперь мы можем решить для \(x\) путем деления обеих сторон на коэффициент квадратного члена:

\((x + \frac{b}{2a})^2 = \frac{4ac - b^2}{4a^2}\)

\(x + \frac{b}{2a} = \sqrt{\frac{4ac - b^2}{4a^2}}\)

\(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)

Это квадратная формула, которая дает корни любого квадратного уравнения вида \( ax^2 + bx + c = 0 \)
Мы также можем использовать квадратную формулу, чтобы проверить, является ли квадратное выражение полным квадратом. Если дискриминант \( b^2 –4ac \) является полным квадратом, то квадратное выражение можно записать в виде полного квадрата. Если дискриминант не является полным квадратом, то квадратное выражение нельзя записать в виде полного квадрата.

Пример:
Рассмотрим квадратное уравнение: \(x^2+6x+1=0\).
Для того чтобы завершить квадрат, мы хотим переписать уравнение в форме \((x+a)^2+b\), где \(a\) и \(b\) - постоянные.
Сначала мы добавим и вычтем \((\frac{b}{2})^2\) \( ( (\frac{6}{2})^2 =9 ) \) к левой части уравнения, чтобы получить:
\(x^2+6x+9-9+1=0\)
Обратите внимание, что первые три члена на левой стороне образуют полный квадратный трехчлен, который мы можем записать как \((x+3)^2\)
Поэтому мы можем переписать уравнение следующим образом: \((x+3)^2-8=0\)
Теперь мы можем решить для \(x\), добавив 8 к обеим сторонам и извлекая квадратный корень:
\((x+3)^2=8 \)
\(x+3=\pm \sqrt{8} \)
\(x=-3 \pm \sqrt{8} \)
Таким образом, решениями исходного уравнения являются:
\(x=-3+ \sqrt{8} \) и \(x=-3- \sqrt{8} \)
И вот как завершить квадрат квадратного уравнения!


Графический метод:
Графический метод - это визуальный метод решения квадратных уравнений. Идея этого метода заключается в построении графика квадратного уравнения и определении \(x\)-перехватов, которые соответствуют решениям уравнения.
Если \(a > 0\), парабола направлена вверх, если \(a < 0\), парабола направлена вниз.
Чтобы построить график квадратного уравнения, сначала перепишем его в форме \( y=ax^2 +bx+c \), где \(y\) - зависимая переменная, а \(x\) - независимая переменная. График квадратного уравнения представляет собой параболу, которая является кривой формы U. Направление и форма параболы зависят от знака коэффициента \(a\). Если \( a > 0 \), парабола открывается вверх, а если \( a < 0 \), парабола открывается вниз.
Чтобы найти \(x\)-перехваты параболы, мы приравниваем \(y=0\) и решаем для \(x\). Это дает нам значения \(x\), где парабола пересекает ось \(x\). Эти значения соответствуют решениям квадратного уравнения.

Рассмотрим пример, чтобы проиллюстрировать этот метод. Предположим, мы хотим решить квадратное уравнение: \(x^2-4x-5=0\).
Мы можем переписать это уравнение в форме \( y=x^2 –4x-5 \) Чтобы построить параболу, мы можем использовать графический калькулятор или программное обеспечение, или мы можем нарисовать его от руки.

График:


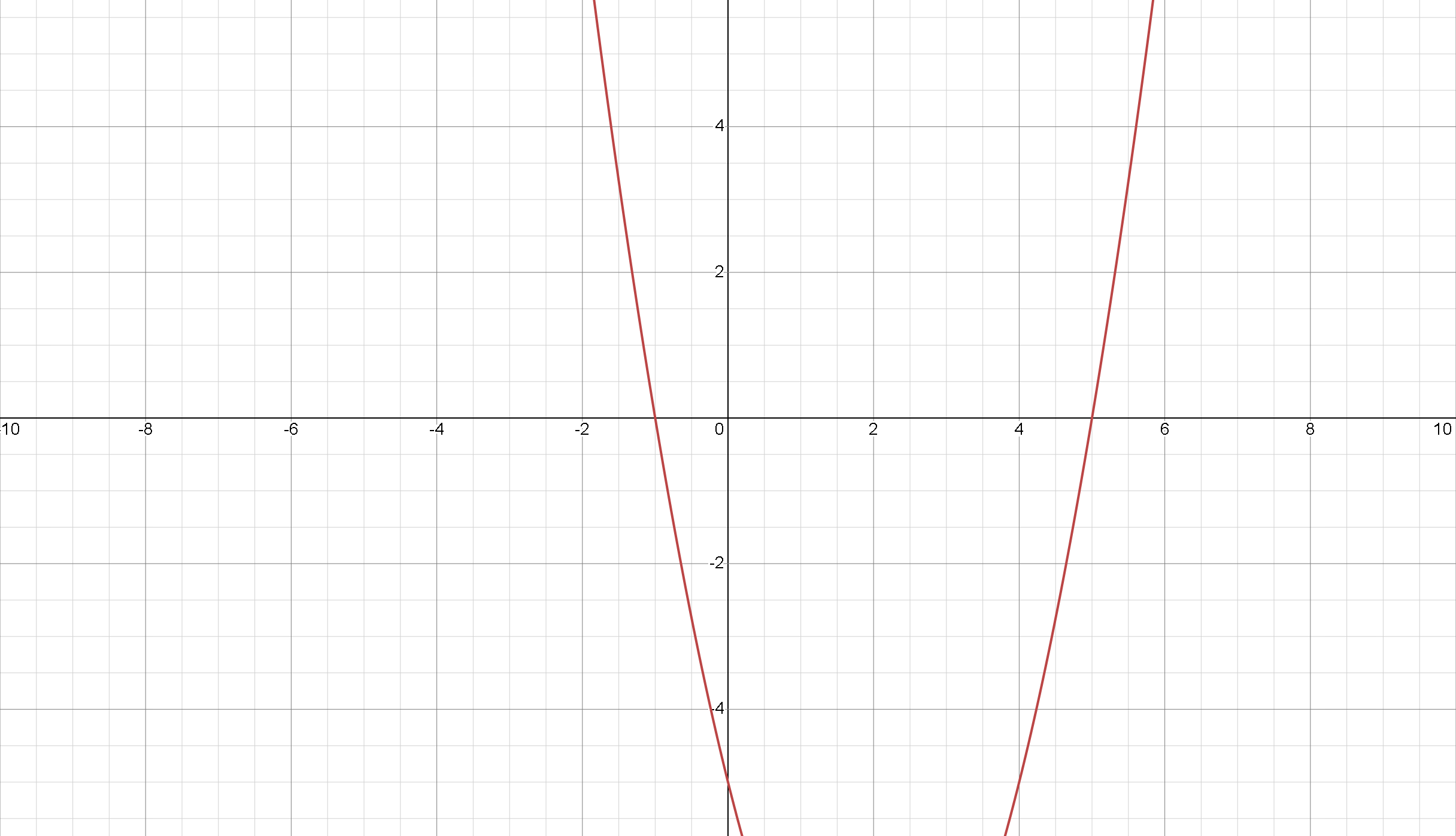
Мы видим, что парабола пересекает ось \(x\) в двух точках, которые соответствуют решениям уравнения. Чтобы найти эти точки, мы можем использовать квадратную формулу или оценить значения \(x\) по графику. В данном случае \(x\)-перехваты примерно равны \(x=-1\) и \(x=5\), которые являются решениями квадратного уравнения.

В заключение, построение графика является полезным методом для визуального решения квадратных уравнений. Построив график уравнения и определив \(x\)-перехваты, мы можем быстро найти решения уравнения.

Формула квадратного уравнения ☰

Формула для корней квадратного уравнения вида \(ax^2+bx+c=0\) известна как квадратная формула. Она задается следующим образом:

\(x =\frac{-b \pm \sqrt{b^2- 4ac}}{2a}\)

Эта формула дает нам значения \(x\), которые являются корнями или решениями квадратного уравнения. Символ \( \pm \) означает, что нам нужно найти как положительные, так и отрицательные корни. Выражение под знаком квадратного корня, \( (b^2 – 4ac) \), называется дискриминантом квадратного уравнения, и оно говорит нам, сколько у уравнения реальных корней.

Если дискриминант положителен \( (b^2 –4ac > 0) \), то у квадратного уравнения есть два различных действительных корня, заданных формулой выше.

Если дискриминант равен нулю \( (b^2 –4ac=0) \), то у квадратного уравнения есть один действительный корень, который задается как \(x=-\frac{b}{2a}\)

Если дискриминант отрицателен \( (b^2 – 4ac < 0) \), то у квадратного уравнения есть два комплексных корня, которые задаются следующим образом:

\(x =\frac{-b \pm i\sqrt{4ac-b^2}}{2a}\) ,

где \(i\) - мнимая единица, равная квадратному корню из \(-1\).
Квадратная формула - это мощный инструмент для решения квадратных уравнений, и ее можно использовать для любого квадратного уравнения, независимо от значений коэффициентов \(a\), \(b\) и \(c\).

Теорема Виета ☰

Теорема Виета, также известная как формулы Виета или связи Виета, является фундаментальной теоремой в алгебре, которая связывает коэффициенты полинома с суммами и произведениями его корней. Теорема названа в честь французского математика Франсуа Виета (латинизированное имя - Франциск Виет), который впервые открыл ее в 16 веке.

Более конкретно, теорема Виета утверждает, что для полинома степени \( n \) с коэффициентами \( a_n, a_{n-1},…, a_1, a_0 \) и корнями \( r_1, r_2,…, r_n \) выполняются следующие отношения: Сумма корней равна отношению противоположного коэффициента и старшего коэффициента:
\( r_1+r_2+ … +r_n=-\frac{a_{n-1}}{a_n} \)

Сумма произведений корней, взятых по два, равна отношению свободного члена и старшего коэффициента с изменением знака в зависимости от четности \( n \):
\( r_1 r_2+r_1 r_3+ … +r_{n-1}r_n=(-1)^n \cdot \frac{a_0}{a_n} \)

Сумма произведений корней, взятых по три, равна отношению коэффициента перед второй по степени и старшего коэффициента с изменением знака в зависимости от четности \( n \): $$ \small r_1 r_2 r_3+r_1 r_2 r_4+ … +r_{n-2} r_{n-1} r_n=(-1)^{n-1} \cdot \frac{a_{n-2}}{a_n} $$

и так далее, где сумма произведений корней, взятых \( k \) за раз, равна
\( (-1)^{n-k} \cdot \frac{a_{n-k}}{a_n} \) для \( k = 1,2,…,n \).

Эти отношения полезны при решении уравнений, содержащих корни полинома, поскольку они позволяют выразить коэффициенты полинома через его корни и наоборот.

Теорему Виета можно применить к квадратным уравнениям, которые являются полиномами второй степени. Для квадратного уравнения вида \(ax^2+bx+c=0\) корни можно найти с помощью квадратной формулы:
\( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)

Используя теорему Виета, мы можем связать корни квадратного уравнения с его коэффициентами следующим образом:

Сумма корней равна противоположному коэффициенту \(x\) деленному на коэффициент \(x^2\):
\( r1+r2=- \frac{b}{a} \)

Произведение корней равно свободному члену деленному на коэффициент \(x^2\):
\( 𝑟1 \cdot 𝑟2= \frac{c}{a} \)

Эти отношения можно вывести, раскрывая квадратное уравнение с помощью свойства дистрибутивности и сравнивая полученное выражение с стандартной формой квадратного уравнения.

Например, предположим, что у нас есть квадратное уравнение \( x^2+5x+6=0 \). Используя квадратную формулу, мы можем найти корни -2 и -3. Используя теорему Виета, мы можем проверить, что эти значения удовлетворяют отношениям:
\( -2+(-3)= -\frac{5}{1} \), что является противоположным коэффициентом \(x\) (5) деленным на коэффициент \(x^2\) (1).
\( -2 \cdot (-3)= \frac{6}{1} \), что является константным членом (6) деленным на коэффициент \( x^2 \) (1).

Эти отношения справедливы для всех квадратных уравнений и полезны при решении задач, которые включают нахождение корней квадратного уравнения или выражение коэффициентов квадратного уравнения через его корни.

Квадратные уравнения могут использоваться для решения широкого спектра задач в различных областях, таких как физика, инженерия, финансы и другие. Вот несколько примеров решения проблем с использованием квадратных уравнений:

• Бросок тела: Тело, запущенное с земли с начальной скоростью \(v0\) и углом \(\theta \), следует параболической траектории, описываемой уравнением $$ y = -\frac{1}{{2g\left(\frac{x}{v_0\cos\theta}\right)^2}} + x\tan\theta $$ где \(g\) - ускорение свободного падения. Это уравнение можно переписать в виде квадратного уравнения относительно \(x\), которое можно использовать для определения горизонтального расстояния, пройденного телом, максимальной высоты, достигнутой им, и времени полета.
• Квадратическая оптимизация: Во многих задачах оптимизации целевая функция может быть выражена как квадратное уравнение, например, $$ f(x)=ax^2+bx+c $$ где \(a > 0\). Чтобы найти максимальное или минимальное значение функции, мы можем использовать формулу вершины, которая дает \(x\)-координату вершины как \( -\frac{b}{2a} \) и соответствующую \(y\)-координату как \(f ( -\frac{b}{2a} ) \)
• Бизнес и финансы: В бизнесе и финансах квадратные уравнения могут использоваться для моделирования различных ситуаций, таких как максимизация прибыли и выручки, минимизация затрат и анализ точки безубыточности. Например, функцию прибыли для продукта можно выразить как $$ P(x)=-ax^2+bx-c $$ где \(x\) - количество проданных единиц, а \(a\), \(b\) и \(c\) - константы. Чтобы найти уровень выпуска, максимизирующий прибыль, мы можем использовать квадратную формулу, чтобы определить значение \(x\), которое максимизирует \(P(x)\)
• Инженерия: В инженерии квадратные уравнения могут использоваться для моделирования и решения различных задач, таких как определение собственной частоты колебательной системы, оптимальное проектирование конструкции или машины, и траектория транспортного средства или ракеты. Например, собственная частота колебательной системы может быть выражена как \( \omega = \sqrt{\frac{k}{m}}\) , где \(k\) - коэффициент упругости, а \(m\) - масса системы. Это уравнение можно переписать так, чтобы получить квадратное уравнение в \( \omega ^2 \), которое можно решить для определения собственной частоты.

Это всего лишь несколько примеров решения задач с использованием квадратных уравнений. В общем, квадратные уравнения можно использовать для моделирования и решения широкого круга задач и являются мощным инструментом во многих областях науки.