Quadratic equations ☰

The general form of a quadratic equation is: $$ ax^2+bx+c=0 $$ where \(a≠0\), \(a\), \(b\) and \(c\) are constants and \(x\) is the variable.
The quadratic equation can be solved using the quadratic formula, which is: $$ x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{{2a}} $$ The quadratic formula provides the solutions for the quadratic equation, which can be real or complex, depending on the discriminant \((b^2–4ac)\). If the discriminant is positive, the quadratic equation has two distinct real roots. If the discriminant is zero, the quadratic equation has one real root, which is a double root. If the discriminant is negative, the quadratic equation has two complex roots.

Incomplete quadratic equations:

If at least one of the coefficients of \(b\) and \(c\) in the quadratic equation \(ax^2+bx+c=0\) is equal to zero, then the equation is called an incomplete quadratic equation.

Solving quadratic equations ☰

There are several methods for solving quadratic equations, including:

• Factoring: This involves writing the quadratic expression as a product of two binomials and setting each binomial equal to zero to find the roots of the equation.
• Completing the square: This involves manipulating the quadratic expression into the form of a perfect square trinomial, and then solving for the roots using basic algebra.
• Quadratic formula: This formula gives the roots of any quadratic equation in terms of its coefficients, and can be derived using the completing the square method.
• Graphing: This involves plotting the quadratic function and identifying the \(x\)-intercepts, which correspond to the roots of the equation.
• Numerical methods: There are several numerical methods that can be used to approximate the roots of a quadratic equation, such as Newton's method, the bisection method, and the secant method.

Each of these methods has its own advantages and disadvantages, and the choice of method depends on the specific problem at hand and the available tools and resources.


Factorization Method of Quadratic Equations:
The factorization method is a technique used to factorize quadratic expressions and solve quadratic equations. To factorize a quadratic expression using this method, we need to find two binomials that multiply together to give the quadratic expression. The general form of a quadratic expression is: $$ ax^2+bx+c $$ To factorize this quadratic expression, we can look for two binomials in the form: $$ (mx+r)(nx+s) $$ where \(m\), \(n\), \(r\) and \(s\) are constants. Expanding the product of these two binomials, we get: $$ mnx^2+(ms+rn)x+rs $$ Comparing this to the general form of the quadratic expression, we can see that:
\(mn=a\)
\(ms+rn=b\)
\(rs=c\)

We can use these equations to solve for \(m, n, r\) and \(s\) -i. Once we have found these constants, we can write the quadratic expression in the factored form as: $$ ax^2+bx+c=(mx+r)(nx+s) $$ To solve a quadratic equation using the factorization method, we can first factorize the quadratic expression as shown above. Once we have factored the quadratic expression, we can use the zero product property to find the roots of the equation. The zero product property states that if the product of two factors is zero, then at least one of the factors must be zero. Therefore, if we have factored the quadratic expression as:
$$ (mx+r)(nx+s)=0 $$ then we can set each factor equal to zero and solve for \(x\): $$ (mx+r)=0 $$ or $$ (nx+s) =0 $$ Solving each linear equation, we get: $$ x=-\frac{r}{m} $$ or $$ x=-\frac{s}{n}$$
Therefore, the roots of the quadratic equation are $$ x=-\frac{r}{m} $$ or $$ x=-\frac{s}{n} $$ It's worth noting that not all quadratic expressions can be factorized using real numbers. In such cases, we may need to use other methods such as completing the square or the quadratic formula to find the roots of the equation.

Example:
Suppose we have the quadratic equation: $$ x^2-5x+6=0 $$ To solve this equation using the factorization method, we need to factor the quadratic expression \( x^2–5x+6 \) into a product of two binomials. We can look for two binomials in the form: $$ (mx+r)(nx+s) $$ where \(m\), \(n\), \(r\) and \(s\) are constants. Expanding the product of these two binomials, we get: $$ mnx^2+(ms+rn)x+rs $$ Comparing this to the quadratic expression \( x^2 –5x+6 \), we can see that:
\(mn=1 \)
\(ms+rn=-5 \)
\(rs=6 \)
We can try different values of \(m\), \(n\), \(r\) and \(s\) until we find values that satisfy these equations.
One possible set of values is \(m=1\), \(n=1\), \(r=-2\) and \(s=-3\) which give: $$ (mx+r)(nx+s) $$ \((x-2)(x-3)=0 \)
Therefore, the roots of the quadratic equation are \(x=2\) and \(x=3\)
We can check that these values are indeed roots of the quadratic equation by substituting them into the original equation
\(2^2-5\cdot 2+6=0 \)
\(3^2-5\cdot 3+6=0 \)
Both of these equations are true, so \(x=2\) and \(x=3\) are indeed roots of the quadratic equation.

Completing the square:
We first need to write the quadratic expression in the form of a complete square. A complete square is an expression of the form $$ (x+a)^2=x^2+2ax+a^2 $$ where \(a\) is a constant. Any quadratic expression can be written in the form of a complete square by adding or subtracting a constant.
Suppose we have a quadratic equation of the form: $$ ax^2+bx+c=0 $$ To solve this equation by dividing a complete square, we first write the quadratic expression as a complete square by adding or subtracting a constant. We can do this by completing the square as follows: $$ a(x^2 + \frac{b}{a}x) = -c $$ $$ a\left(x^2 + \frac{b}{a}x + \frac{b^2}{4a^2}\right) = -c + a(\frac{b^2}{4a^2}) $$ $$ a\left(x + \frac{b}{2a}\right)^2 = \frac{4ac - b^2}{4a} $$ We can now solve for \(x\) by dividing both sides by the coefficient of the square term: $$ (x + \frac{b}{2a})^2 = \frac{4ac - b^2}{4a^2} $$ $$ x + \frac{b}{2a} = \sqrt{\frac{4ac - b^2}{4a^2}} $$ $$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$ This is the quadratic formula, which gives the roots of any quadratic equation of the form $$ ax^2 + bx + c = 0 $$ We can also use the quadratic formula to check whether a quadratic expression If the discriminant \( b^2 –4ac \) is a perfect square, then the quadratic expression can be written in the form of a complete square. If the discriminant is not a perfect square, then the quadratic expression cannot be written in the form of a complete square.

Example:
Let's consider the quadratic equation: \(x^2+6x+1=0\).
To complete the square, we want to rewrite the equation in the form of \((x+a)^2+b\), where \(a\) and \(b\) are constants.
First, we'll add and subtract $$(\frac{b}{2})^2 $$ $$ ( (\frac{6}{2})^2 =9 ) $$ to the left-hand side of the equation to get:
\(x^2+6x+9-9+1=0\)
Notice that the first three terms on the left-hand side form a perfect square trinomial, which we can write as \((x+3)^2\)
So we can rewrite the equation as: \((x+3)^2-8=0\)
Now we can solve for x by adding 8 to both sides and taking the square root:
\((x+3)^2=8 \)
\(x+3=\pm \sqrt{8} \)
\(x=-3 \pm \sqrt{8} \)
So the solutions to the original equation are:
\(x=-3+ \sqrt{8} \) and \(x=-3- \sqrt{8} \)
And that's how to complete the square of a quadratic equation!

Graphing:
Graphing is a visual method for solving quadratic equations. The idea behind this method is to graph the quadratic equation and identify the \(x\)-intercepts, which correspond to the solutions of the equation.
Əgər \(a > 0\) olarsa, parabola yuxarıya, \(a < 0\) olarsa, aşağıya doğru açılır.
To graph a quadratic equation, we first rewrite it in the form \( y=ax^2 +bx+c \), where \(y\) is the dependent variable and \(x\) is the independent variable. The graph of a quadratic equation is a parabola, which is a U-shaped curve. The direction and shape of the parabola depend on the sign of the coefficient \(a\). If \( a > 0 \), the parabola opens upwards, and if \( a < 0 \), the parabola opens downwards.
To find the \(x\)-intercepts of the parabola, we set \(y=0\) and solve for \(x\). This gives us the values of \(x\) where the parabola intersects the \(x\)-axis. These values correspond to the solutions of the quadratic equation.

Let's consider an example to illustrate this method. Suppose we want to solve the quadratic equation: $$ x^2-4x-5=0 $$ We can rewrite this equation in the form \( y=x^2 –4x-5 \) To graph the parabola, we can use a graphing calculator or a software program, or we can sketch it by hand.

Graph:


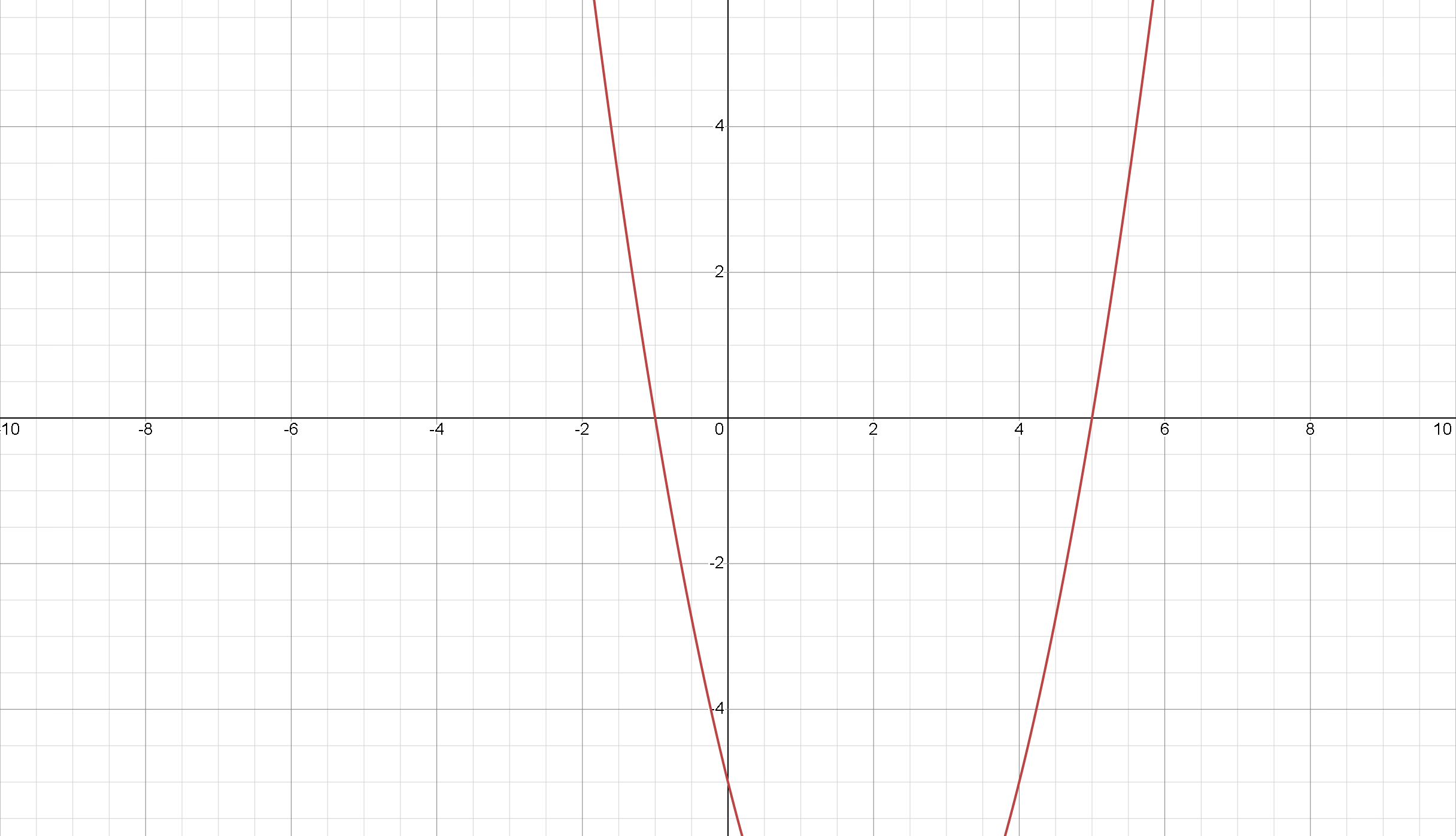
We can see that the parabola intersects the \(x\)-axis at two points, which correspond to the solutions of the equation. To find these points, we can either use the quadratic formula or estimate the \(x\)-values from the graph. In this case, the \(x\)-intercepts are approximately \(x=-1\) and \(x=5\), which are the solutions of the quadratic equation.

In summary, graphing is a useful method for solving quadratic equations visually. By graphing the equation and identifying the x-intercepts, we can quickly find the solutions of the equation.

Quadratic formula ☰

The formula for the roots of a quadratic equation of the form $$ ax^2+bx+c=0 $$ is known as the quadratic formula. It is given by: $$ x =\frac{-b \pm \sqrt{b^2- 4ac}}{2a} $$ This formula gives us the values of \(x\), which are the roots or solutions of the quadratic equation. The symbol \( \pm \) means that we need to find both the positive and negative roots. The expression inside the square root, $$ (b^2 – 4ac) $$ is called the discriminant of the quadratic equation, and it tells us how many real roots the equation has.

If the discriminant is positive $$ (b^2 –4ac > 0) $$ the quadratic equation has two distinct real roots, given by the formula above.

If the discriminant is zero $$ (b^2 –4ac=0) $$ the quadratic equation has one real root, which is given by \(x=-\frac{b}{2a}\)

If the discriminant is negative \( (b^2 – 4ac < 0) \), the quadratic equation has two complex roots, which are given by: $$ x=\frac{-b \pm i\sqrt{4ac-b^2}}{2a} $$ where \(i\) is the imaginary unit, equal to the square root of \(-1\).
The quadratic formula is a powerful tool for solving quadratic equations, and it can be used for any quadratic equation, regardless of the values of the coefficients \(a\), \(b\) and \(c\).

Viet's theorem: ☰

Viet's theorem, also known as Vieta's formulas or Vieta's relations, is a fundamental theorem in algebra that relates the coefficients of a polynomial to the sums and products of its roots. The theorem is named after French mathematician François Viète (Latinized as Franciscus Vieta), who first discovered it in the 16th century.

More specifically, Viet's theorem states that for a polynomial of degree n with coefficients \( a_n,a_{n-1},…,a_1,a_0 \) and roots \( r_1,r_2,…,r_n \), the following relationships hold: The sum of the roots is equal to the ratio of the opposite coefficient and the leading coefficient: $$ r_1+r_2+ … +r_n=-\frac{a_{n-1}}{a_n} $$

The sum of the products of the roots taken two at a time is equal to the ratio of the constant term and the leading coefficient with a sign change according to the parity of \(n\): $$ r_1 r_2+r_1 r_3+ … +r_{n-1}r_n=(-1)^n \cdot \frac{a_0}{a_n} $$

The sum of the products of the roots taken three at a time is equal to the ratio of the coefficient of the second-to-highest power and the leading coefficient with a sign change according to the parity of \(n\): $$ r_1 r_2 r_3+r_1 r_2 r_4+ … +r_{n-2} r_{n-1} r_n=(-1)^{n-1} \cdot \frac{a_{n-2}}{a_n} $$

and so on, with the sum of the products of the roots taken k at a time being equal to $$ (-1)^{n-k} \cdot \frac{a_{n-k}}{a_n} $$ for \( k = 1,2,…,n \).

These relationships are useful in solving equations involving polynomial roots, as they allow one to express the coefficients of a polynomial in terms of its roots and vice versa.

Viet's theorem can be applied to quadratic equations, which are polynomials of degree 2. For a quadratic equation of the form \(ax^2+bx+c=0\), the roots can be found using the quadratic formula: $$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

Using Viet's theorem, we can relate the roots of the quadratic equation to its coefficients as follows:

The sum of the roots is equal to the opposite of the coefficient of \(x\) divided by the coefficient of \( x^2 \): $$ r1+r2=- \frac{b}{a} $$ The product of the roots is equal to the constant term divided by the coefficient of \(x^2\): $$ 𝑟1 \cdot 𝑟2= \frac{c}{a} $$ These relationships can be derived by expanding the quadratic equation using the distributive property and comparing the resulting expression to the standard form of a quadratic equation.

For example, suppose we have the quadratic equation \( x^2+5x+6=0 \). Using the quadratic formula, we can find the roots to be -2 and -3. Using Viet's theorem, we can verify that these values satisfy the relationships: $$ -2+(-3)= -\frac{5}{1} $$ which is the opposite of the coefficient of \(x\) (5) divided by the coefficient of \(x^2\) (1). $$-2 \cdot (-3)= \frac{6}{1} $$ which is the constant term (6) divided by the coefficient of \( x^2 \) (1).

These relationships hold for all quadratic equations and are useful in solving problems that involve finding the roots of a quadratic equation or expressing the coefficients of a quadratic equation in terms of its roots.

Quadratic equations can be used to solve a wide range of problems in various fields , such as physics, engineering, finance, and more. Here are a few examples of problem solving using quadratic equations:

• Projectile motion: A projectile launched from the ground with an initial velocity \(v0\) and angle \(\theta \) follows a parabolic trajectory described by the equation $$ y = -\frac{1}{{2g\left(\frac{x}{v_0\cos\theta}\right)^2}} + x\tan\theta $$ here \(g\) is the acceleration due to gravity. This equation can be rewritten as a quadratic equation in \(x\), which can be used to determine the horizontal distance traveled by the projectile, the maximum height reached, and the time of flight.
• Quadratic optimization: In many optimization problems, the objective function can be expressed as a quadratic equation, such as $$ f(x)=ax^2+bx+c $$ where \(a > 0\). To find the maximum or minimum value of the function, we can use the vertex formula, which gives the \(x\)-coordinate of the vertex as $$ -\frac{b}{2a} $$ and the corresponding \(y\)-coordinate as $$ f ( -\frac{b}{2a} ) $$
• Business and finance: In business and finance, quadratic equations can be used to model various situations, such as profit and revenue maximization, cost minimization, and break-even analysis. For example, the profit function for a product can be expressed as $$ P(x)=-ax^2+bx-c $$ where \(x\) is the number of units sold and \(a\), \(b\) and \(c\) are constants. To find the profit-maximizing level of output, we can use the quadratic formula to determine the value of \(x\) that maximizes \(P(x)\)
• Engineering: In engineering, quadratic equations can be used to model and solve various problems, such as determining the natural frequency of a vibrating system, the optimal design of a structure or machine, and the trajectory of a vehicle or missile. For example, the natural frequency of a vibrating system can be expressed as \( \omega = \sqrt{\frac{k}{m}}\) , where \(k\) is the spring constant and \(m\) is the mass of the system. This equation can be rearranged to give a quadratic equation in \( \omega ^2 \), which can be solved to determine the natural frequency.

These are just a few examples of problem solving using quadratic equations. In general, quadratic equations can be used to model and solve a wide range of problems, and are a powerful tool in many fields of study.