Dönmə bucaqları ☰

Fırlanma bucağı, fırlanma mərkəzi adlanan sabit bir nöqtə ətrafında bir fiqurun fırlanma miqdarını təsvir etmək üçün həndəsədə istifadə olunan bir anlayışdır. Fiqur fırlandıqda, fiqurun bütün nöqtələri fırlanma mərkəzi ətrafında dairəvi yollar boyunca hərəkət edir və fırlanma bucağı rəqəmin məruz qaldığı dərəcə və ya radianla ölçülən fırlanma miqdarıdır.

Fırlanma bucağını riyazi olaraq təyin etmək üçün vahid dairə anlayışından istifadə etməliyik. Vahid çevrə radiusu 1 olan Dekart müstəvisinin başlanğıcında mərkəzləşmiş çevrədir. Biz əsas triqonometrik funksiyalar olan bucağın sinus və kosinus funksiyalarını təyin etmək üçün vahid dairədən istifadə edə bilərik.

Fərz edək ki, vahid dairədə aşağıdakı şəkildə göstərildiyi kimi müsbət \(x\) oxu ilə \( \theta \) bucağı yaradan \((x,y)\) nöqtəsi var:

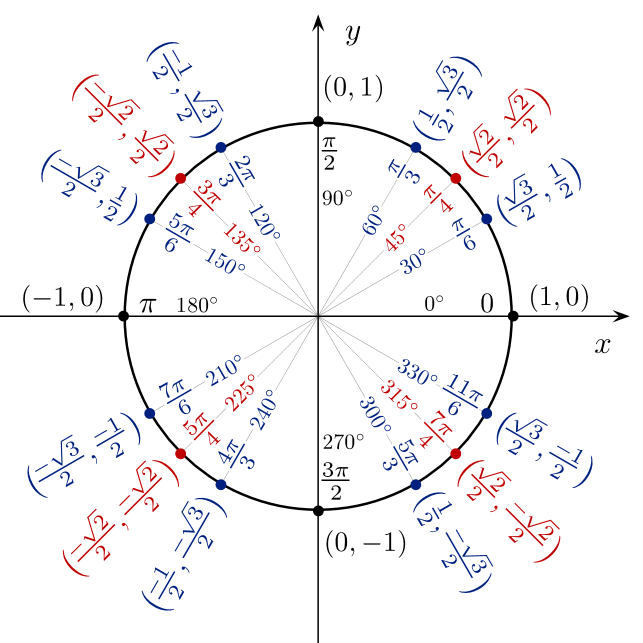
Onda nöqtənin koordinatları belə verilir:
\( x = cos( \theta ) \), \( y = sin( \theta) \).
Fırlanma bucağı aşağıdakı kimi müəyyən edilə bilər. Tutaq ki, müstəvidə \(F\) fiqurumuz var və biz fiquru sabit O nöqtəsi ətrafında saat əqrəbinin əksinə \( \theta \) bucağı ilə fırladıq. Bu fırlanma altında \(F\)-in şəkli \(F'\) olsun. Sonra fırlanma bucağı hər ikisi \(O\) fırlanma mərkəzində kəsişən \(F\) və \(F'\) hər hansı iki uyğun xətt seqmenti arasındakı bucaq kimi müəyyən edilir.

Fırlanma bucağını vahid dairənin üzərindəki nöqtələrin koordinatları ilə ifadə edə bilərik. Tutaq ki, F üzərində O ətrafında saat əqrəbinin əksi istiqamətində \( \theta \) bucağı ilə fırlanan \( P = (x,y) \) nöqtəsi var və \( P' = (x', y' ) \) də \(F' \) üzərində uyğun nöqtə olsun. Sonra fırlanma bucağı aşağıdakı düsturla hesablana bilər:
\( \theta = \cos^{-1}\left(\frac{xx' + yy'}{\sqrt{x^2 + y^2} \sqrt{{x'}^2 + {y'}^2}}\right) \)

Xülasə, fırlanma bucağı sabit bir nöqtə ətrafında fiqura tətbiq edilən fırlanma miqdarının ölçüsüdür və o, nöqtə məhsulu düsturundan istifadə etməklə və ya orijinal və fırlanan fiqurların müvafiq xətt seqmentləri arasındakı bucağı ölçməklə hesablana bilər.

Bucağın radian və dərəcə ölçüsü ☰

Bucaq, təpə adlanan ümumi son nöqtəni paylaşan iki şüa və ya xətt seqmentindən əmələ gələn həndəsi fiqurdur. Bucaqlar müxtəlif vahidlərlə ölçülə bilər, lakin ən çox yayılmış vahidlər radian və dərəcədir.
Radianlar bir dairənin qövsünün uzunluğuna əsaslanan bucaq ölçü vahididir. Bir radian, dairənin radiusuna bərabər uzunluqlu bir qövsdən keçən bucaq kimi müəyyən edilir. Başqa sözlə, əgər çevrənin radiusu r olarsa, onda çevrənin mərkəzindəki bir radianlıq bucaq r uzunluğunda bir qövsə uyğun gələcək. Radianların simvolu "rad"dır.
Dərəcələr dairənin hər biri bir dərəcə olmaqla 360 bərabər hissəyə bölünməsinə əsaslanan digər bucaq ölçü vahididir. Dərəcələrin simvolu "\( ^\circ \)"-dir. Dairə ətrafında bir tam çevrilmə 360 dərəcəyə \( (360^\circ ) \) bərabərdir.
Radian və dərəcə arasında çevirmək üçün aşağıdakı düsturlardan istifadə edə bilərik:

• Radianlardan dərəcələrə çevirmək üçün: bucağı \( \frac{180}{\pi} \) ilə vurun.
• Dərəcələrdən radiana çevirmək üçün: bucağı \( \frac{\pi}{180} \) ilə vurun.

Məsələn, \( \theta = 2 \) radian bucağı dərəcəyə çevirmək üçün:
\( \theta = \text{radian} \cdot \frac{180}{\pi} = 2 \cdot \frac{180}{\pi} \approx 114.59^\circ \)

Eyniylə, \( \theta = 45^\circ \) bucağı radiana çevirmək üçün:
\( \theta = \text{dərəcə} \cdot \frac{\pi}{180} = 45 \cdot \frac{\pi}{180} = \frac{\pi}{4} \approx 0.7854 \text{ rad} \)

Xülasə, radianlar və dərəcələr həndəsədə bucaqları ölçmək üçün istifadə olunan iki ümumi bucaq ölçü vahididir. Radianlar çevrənin qövsünün uzunluğuna, dərəcələr isə dairənin 360 bərabər hissəyə bölünməsinə əsaslanır. Yuxarıda qeyd olunan düsturlardan istifadə edərək radyan və dərəcə arasında çevirmə edə bilərik.

Triqonometrik funksiyalar və vahid çevrə ☰

Triqonometrik funksiyalar üçbucağın bucaqlarını onun tərəflərinin uzunluqları ilə əlaqələndirən riyazi funksiyalardır. Ən çox istifadə edilən triqonometrik funksiyalar sinus, kosinus və tangensdir. Bu funksiyalar tez-tez vahid çevrədən istifadə etməklə təmsil olunur ki, bu da Dekart koordinat sisteminin başlanğıcında mərkəzləşdirilmiş radiusu 1 olan çevrədir.
Vahid dairə faydalıdır, çünki bucaqlar və triqonometrik funksiyalar arasındakı əlaqələri asanlıqla vizuallaşdırmağa imkan verir. Başlanğıcdan vahid dairənin bir nöqtəsinə xətt çəksək, bu xətt ilə müsbət \(x\) oxu arasındakı bucaq fırlanma bucağı və ya sadəcə olaraq bucaq kimi tanınır. Xəttin vahid dairə ilə kəsişdiyi nöqtə sinus, kosinus və tangensin xüsusi dəyərinə uyğundur.
Üç əsas triqonometrik funksiyanın tərifləri aşağıdakılardır:

• Sinus (sin): Düzbucaqlı üçbucaqda bucağın qarşı tərəfin uzunluğunun hipotenuzun uzunluğuna olan nisbəti. Başqa sözlə desək, mərkəzi koordinat başlanğıcında olan, r radiuslu çevrə üzərindəki müəyyən nöqtənin ordinatının radiusun uzunluğuna olan nisbəti.
• Kosinus (cos): Bucağa bitişik tərəfin uzunluğunun düzbucaqlı üçbucağın hipotenuzun uzunluğuna nisbəti. Başqa sözlə desək, mərkəzi koordinat başlanğıcında olan, r radiuslu çevrə üzərindəki müəyyən nöqtənin absisinin radiusun uzunluğuna olan nisbəti.
• Tangens (tg): Mərkəzi koordinat başlanğıcında olan, r radiuslu çevrə üzərindəki müəyyən nöqtənin ordinatının absisinə olan nisbəti.

Vahid çevrədən istifadə edərək digər üç triqonometrik funksiyanı da təyin edə bilərik: kosekant (csc), sekant (sec) və kotangent (ctg). Bunlar sadəcə olaraq sinus, kosinus və tangensin əksidir.
Sinus, tangens, kotangens funksiyaları tək, kosinus isə cüt funksiyadır.

İstənilən bucağın triqonometrik funksiyası ☰

Triqonometrik funksiyalar yalnız düzbucaqlı üçbucaqlardakı bucaqlar üçün deyil, istənilən bucaq üçün müəyyən edilə bilər. Vahid çevrədəki bucağın triqonometrik funksiyalarının tərifləri aşağıda verilmişdir:
Standart vəziyyətdə \( \theta \) bucağını nəzərdən keçirək, yəni müsbət x oxundan başlayır və saat əqrəbinin əksi istiqamətində fırlanır.
\( \theta \) bucağının son tərəfinin koordinat başlanğıcında mərkəzləşmiş vahid dairə ilə kəsişdiyi nöqtə \( (x,y) \) olsun.
Sinus (sin): \( sin(\theta ) = y \)
Kosinus (cos): \( cos( \theta ) = x \)
Tangens (tg): \( tg( \theta ) = \frac{y}{x} \), \(x \neq 0 \)

Digər triqonometrik funksiyalar aşağıdakı kimidir:
Kosekans (cosec): \( cossec( \theta ) = \frac{1}{sin \theta } \)
Sekans (sec): \( sec(\theta ) = \frac{1}{cos \theta } \)
Kotangens (ctg): \( ctg(\theta ) = \frac{1}{tg \theta } \)

Triqonometrik funksiyaların qiymətləri \( \theta \) bucağının yerləşdiyi rübdən asılı olaraq müsbət, mənfi və ya sıfır ola bilər. Birinci rübdə \( ( 0 < θ < 90 \text{ dərəcə} ) \) altı triqonometrik funksiyanın hamısı müsbətdir.
İkinci rübdə \(( 90 < θ < 180 \text{ dərəcə}) \) yalnız sinus müsbətdir. Üçüncü rübdə \( (180 < θ < 270 \text{ dərəcə}) \) yalnız tangens müsbətdir. Dördüncü rübdə \( (270 < θ < 360 \text{ dərəcə}) \) yalnız kosinus müsbətdir.
Unutmayın ki, bucaqlar dərəcə və ya radyanla ölçülə bilər. Radianlar bucaqları ölçmək üçün başqa bir yoldur, burada bir radian dairənin radiusuna bərabər uzunluqlu bir qövsü əhatə edən bucaq kimi müəyyən edilir. Dərəcələr və radyanlar arasında çevrilmə aşağıdakı kimi verilir:
\(\pi \text{ radian} = 180 \text{ dərəcə} \)
\( \text{1 radian } \approx 57.3 \text{ dərəcə} \)
\( \text{1 dərəcə } \approx 0.0175 \text{ radian} \)
Radianla ölçülən bucaqların triqonometrik funksiyaları ilə işləyərkən bu bucaqları ifadə etmək üçün rahat üsul kimi yunan hərfindən \(\pi \) (pi) istifadə edirik.
Məsələn, 90 dərəcə bucaq \( \frac{\pi}{2} \) radian, 180 dərəcə bucaq isə \(\pi \) radian kimi ifadə edilə bilər.

Çevirmə düsturları ☰

Fırlanma düsturları koordinat sistemindəki sabit nöqtə ətrafında verilmiş bucaqla fırlandıqdan sonra onun yeni koordinatlarını hesablamaq üçün istifadə olunan tənliklər toplusudur. Xüsusi problemdən asılı olaraq bu düsturların bir neçə variantı var, lakin biz onların arxasında duran əsas fikri anlamağa çalışacağıq.

Tutaq ki, koordinat sistemində koordinatları \( (x,y) \) olan \(P\) nöqtəsi var. Biz bu nöqtəni sabit O nöqtəsi, koordinat başlanğıcı (fırlanma başlanğıcı adlanır) ətrafında \( \theta \) bucağı ilə fırlatmaq istəyirik. Məqsəd bu fırlanmadan sonra P-nin yeni koordinatlarını \( (x', y' ) \) tapmaqdır.

Bunun üçün yeni koordinatları orijinal koordinatlara və fırlanma bucağına aid edən bir sıra tənliklərdən istifadə edirik. Bu tənlikləri əldə etməyin bir yolu əsas triqonometriyadan istifadə etməkdir. Konkret olaraq, fırlanma mərkəzi O, orijinal P nöqtəsi və fırlanan P nöqtəsi ilə əmələ gələn üçbucağı nəzərdən keçirə bilərik. Bu üçbucağın tərəfləri x, y və r uzunluqlarına malikdir (O-dan P-yə qədər olan məsafə) və \(x\) oxu ilə \(OP\) xətti arasındakı bucaq \(\phi \)-dir. Fırlanmadan sonra \(x\) oxu ilə \(OP' \) xətti arasındakı bucaq \( \phi + \theta \) olur.

Triqonometriyadan istifadə edərək yeni koordinatları \( (x', y' ) \) , ilkin koordinatlar \( (x , y ) \) və fırlanma bucağı \( \theta \) ilə aşağıdakı kimi ifadə edə bilərik:
\( x' = xcos(\theta ) - ysin( \theta ) \)
\( y' = xsin( \theta ) + ycos( \theta ) \)
Bu tənliklər bizə P-nin O ətrafında \( \theta \) bucağı ilə fırlanmasından sonra P'-nin yeni koordinatlarını verir.

Koordinat başlanğıcından başqa bir nöqtə ətrafında fırlanma:
Əsas fırlanma düsturları P nöqtəsinin koordinat başlanğıcı ətrafında fırlandığını nəzərdə tutur. Əgər nöqtəni fərqli Q nöqtəsi ətrafında çevirmək istəsək, əvvəlcə koordinat sistemini elə çevirə bilərik ki, Q mənbəyə çevrilsin, sonra əsas düsturları tətbiq edək və nəhayət koordinat sistemini geri çevirə bilərik. Alternativ olaraq, Q nöqtəsinin koordinatlarını nəzərə alan fırlanma düsturlarının daha ümumi formasından istifadə edə bilərik. Məsələn, P nöqtəsini Q nöqtəsi ətrafında \( (a , b ) \) koordinatları ilə \( \theta \) bucağı ilə çevirmək istəsək, yeni koordinatları \( ( x' , y' ) \) aşağıdakı kimi hesablamaq olar:
\( x' = (x-a) \cdot cos(\theta ) - (y-b) \cdot sin(\theta ) + a \)
\( y' = (x-a) \cdot sin(\theta ) + (y-b) \cdot cos(\cdot ) + b \)

Qeyd edək ki, cədvəldə \( (x,y) \) nöqtəsi fırlanmadan əvvəl orijinal təsvirdəki nöqtənin koordinatlarını, üçüncü sütundakı nöqtə isə fırlanmadan sonra eyni nöqtənin koordinatlarını təmsil edir. Fırlanma bucağı dərəcələrlə ölçülür və "saat yönündə" və "saat əqrəbinin əksinə" istiqamətləri başlanğıc ətrafında fırlanma istiqamətinə aiddir.

Triqonometrik eyniliklər ☰

Triqonometrik eyniliklər triqonometrik funksiyaları (sinus, kosinus, tangens və s.) əhatə edən və cəlb olunan dəyişənlərin bütün mümkün qiymətləri üçün doğru olan riyazi tənliklərdir. Bu eyniliklər triqonometriyada və hesablamada triqonometrik funksiyaları əhatə edən ifadələri sadələşdirmək və manipulyasiya etmək üçün geniş şəkildə istifadə olunur.


Ən vacib triqonometrik eyniliklərdən bəziləri bunlardır:

Pifaqor eyniliyi:
\( sin^2 (x) + cos^2 (x) = 1 \)

Bu eynilik sinus və kosinus funksiyalarını əlaqələndirir və onların kvadratlarının cəminin həmişə birə bərabər olduğunu ifadə edir. Düzbucaqlı üçbucağın katetlərinin uzunluqlarının kvadratlarının cəminin hipotenuzun uzunluğunun kvadratına bərabər olduğunu bildirən Pifaqor teoremindən götürülmüşdür.

Qarşılıqlı eyniliklər:
\( sin(x) = \frac{1}{csc(x)} \)

\( cos(x) = \frac{1}{sec(x)} \)

\( tg(x) = \frac{1}{ctg(x)} \)

Bu eyniliklər triqonometrik funksiyalar və onlara uyğun qarşılıqlı funksiyalar (kosekant, sekant və kotangent) arasındakı qarşılıqlı əlaqəni ifadə edir. Məsələn, birinci eynilik bucağın sinusunun həmin bucağın kosekantının əksinə bərabər olduğunu bildirir.

Cüt-tək eyniliyi:
\( sin(-x) = -sin(x) \)
\( cos(-x) = cos(x) \)

Cəm və fərq:
\( sin(x+y) = sin(x) cos(y) + cos(x)sin(y) \)
\( sin(x-y) = sin(x) cos(y) - cos(x)sin(y) \)
\( cos(x+y) = cos(x) cos(y) - sin(x)sin(y) \)
\( cos(x-y) = cos(x) cos(y) + sin(x)sin(y) \)

Bu eyniliklər ayrı-ayrı bucaqların triqonometrik funksiyaları baxımından iki bucağın cəmi və fərqinin triqonometrik funksiyalarını ifadə edir. Onlar triqonometrik funksiyaları əhatə edən ifadələri sadələşdirmək üçün hesablamalarda və riyaziyyatın digər sahələrində geniş istifadə olunur.

İkiqat bucaq:
\( sin (2x) = 2 sin (x) cos (x) \)

\( \small cos(2x) = cos^2 (x) - sin^2 (x) = \) \( \small 2cos^2 (x) - 1 = 1-2 sin^2 (x) \)

Yarım bucaq:
\( sin( \frac{x}{2} ) = \pm \sqrt{ \frac{1- cos x}{2} } \)

\( cos( \frac{x}{2} ) = \pm \sqrt{ \frac{1+ cos x}{2} } \)

\( tan( \frac{x}{2} ) = \pm \sqrt{ \frac{1- cos x}{1+ cos x} } \)

Vurmadan toplamaya:
\( sin(x)sin(y) = \frac{1}{2} [cos(x-y) - cos(x+y) ] \)

\( cos(x) cos(y) = \frac{1}{2} [cos(x-y) + cos(x+y) ] \)

\( sin(x) cos(y) = \frac{1}{2} [sin(x+y) + sin(x-y) ] \)

Toplamadan vurmaya:
\( sin(x) + sin(y) = 2 sin [ \frac{x+y}{2} ] cos [ \frac{x-y}{2} ] \)

\( sin (x) - sin (y) = 2 cos [ \frac{x+y}{2} ] sin [ \frac{x-y}{2} ] \)

\( cos(x) + cos(y) = 2 cos[ \frac{x+y}{2} ] cos[ \frac{x-y}{2} ] \)

\( cos(x)-cos(y) = -2sin[ \frac{x+y}{2} ] sin[ \frac{x-y}{2} ] \)

Kofunksiya:
\( sin(x) = cos( 90^\circ - x) \)
\( cos(x) = sin( 90^\circ - x) \)
\( tan(x) = ctg( 90^\circ - x) \)
\( ctg(x) = tan( 90^\circ - x) \)

Dövrilik:
\( sin(x + 2 \pi) = sin(x) \)
\( cos(x + 2 \pi ) = cos(x) \)
\( tan(x + \pi ) = tan(x) \)

Bu eynilik triqonometrik funksiyaların dövri xarakterini ifadə edir. Sinus və kosinus funksiyaları hər \( 2 \pi \) radiandan bir, tangens funksiyası isə hər \( \pi \) radiandan bir təkrarlanır.
Bunlar riyaziyyatda istifadə olunan ən vacib triqonometrik eyniliklərdən bəziləridir. Bu eynilikləri əzbərləmək və onların necə tətbiq olunacağını başa düşməklə tələbələr triqonometriyada bacarıqlı ola və triqonometrik funksiyaları əhatə edən çətin məsələləri həll edə bilərlər.

Triqonometrik ifadələrin sadələşdirilməsi ☰

Triqonometrik ifadələrin sadələşdirilməsi, işləmək daha asan olan daha sadə formada olana qədər cəbri manipulyasiyanı nəzərdə tutur. Triqonometrik ifadəni sadələşdirmək üçün müxtəlif triqonometrik eyniliklərdən və xassələrdən istifadə edilməlidir. Öncəki başlıqda qeyd edilən eyniliklərdən triqonometrik funksiyaları sadələşdirmək üçün istifadə edilir.

Bu eyniliklərdən istifadə edərək, bir triqonometrik ifadəni ən sadə formada olana qədər addım-addım sadələşdirmək olar. Triqonometrik ifadələrin sadələşdirilməsinə bəzi nümunələr bunlardır:

\( sin^2 (x) + cos^2 (x) \rightarrow 1 \)

\( \frac{sin^2 (x)}{1 - cos (x)} \rightarrow \frac{1+cos(x)}{2-cos(x)} \)

\( \frac{sin (x)}{cos (x)} - \frac{cos (x)}{sin (x)} \rightarrow \frac{sin^2 (x) - cos^2 (x)}{sin (x) cos (x)} \)

\( \frac{sin (x)}{cos (x) + 1} + \frac{1}{cos (x) - 1} \rightarrow \frac{2 sin(x)}{cos^2 (x) - 1} \)

Qeyd etmək lazımdır ki, triqonometrik ifadələri sadələşdirərkən ifadənin oblastına diqqət yetirmək lazımdır. Bəzi triqonometrik funksiyalar bucağın müəyyən qiymətləri üçün müəyyən edilməyib, məsələn, \( \theta = \frac{\pi}{2} + k \pi \) üçün \( tg( \theta ) \) və \( ctg( \theta ) \), burada \(k\) tam ədəddir. Bundan əlavə, bəzi eyniliklər yalnız bucağın müəyyən qiymətləri üçün və ya müəyyən şərtlər yerinə yetirildikdə etibarlıdır.
Məsələn, yarım bucaq eynilikləri yalnız \( \frac{\pi }{2} \le \theta \le \pi \) və \(cos(\theta ) \ge 0 \) üçün etibarlıdır.