Angle de rotation ☰

L'angle de rotation est un concept utilisé en géométrie pour décrire la quantité de rotation appliquée à une figure autour d'un point fixe appelé le centre de rotation. Lorsqu'une figure est tournée, tous les points de la figure se déplacent le long de chemins circulaires autour du centre de rotation, et l'angle de rotation est la quantité de rotation, mesurée en degrés ou en radians, que subit la figure.

Pour définir mathématiquement l'angle de rotation, nous devons utiliser le concept du cercle unité. Le cercle unité est un cercle centré à l'origine du plan cartésien avec un rayon de 1. Nous pouvons utiliser le cercle unité pour définir les fonctions sinus et cosinus d'un angle, qui sont des fonctions trigonométriques fondamentales.

Supposons que nous ayons un point \((x,y) \) sur le cercle unité qui forme un angle \( \theta \) avec l'axe \(x\) positif, comme illustré dans la figure ci-dessous:

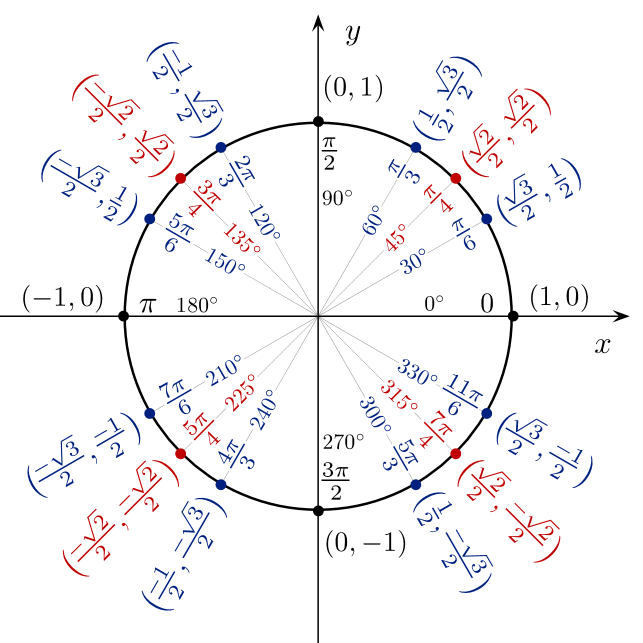
Alors les coordonnées du point sont données par:
\( x = \cos( \theta ) \), \( y = \sin( \theta) \).

L'angle de rotation peut être défini comme suit. Supposons que nous ayons une figure \(F\) dans le plan, et que nous tournions la figure dans le sens antihoraire autour d'un point fixe \(O\) d'un angle \( \theta \). Soit \(F' \) l'image de \(F\) sous cette rotation. Alors l'angle de rotation est défini comme l'angle entre deux segments de droite correspondants de \(F \) et \(F' \) , qui intersectent tous les deux au centre de rotation \(O\).
Nous pouvons exprimer l'angle de rotation en termes des coordonnées des points sur le cercle unité. Supposons que nous ayons un point \(P=(x,y) \) sur \(F\) qui tourne dans le sens antihoraire autour de \(O\) d'un angle \( \theta \), et soit \(P'=(x',y' ) \) le point correspondant sur \(F' \). Alors l'angle de rotation peut être calculé en utilisant la formule suivante:

\( \theta = \cos^{-1}\left(\frac{xx' + yy'}{\sqrt{x^2 + y^2} \sqrt{{x'}^2 + {y'}^2}}\right) \)

Cette formule est dérivée de la formule du produit scalaire pour l'angle entre deux vecteurs. Le numérateur de la fraction est le produit scalaire des vecteurs \(OP\) et \(OP'\), et le dénominateur est le produit de leurs magnitudes.

En résumé, l'angle de rotation est une mesure de la quantité de rotation appliquée à une figure autour d'un point fixe, et il peut être calculé en utilisant la formule du produit scalaire ou en mesurant l'angle entre des segments de droite correspondants des figures originale et tournée.

Mesure en degrés et en radians ☰

Un angle est une figure géométrique formée par deux rayons ou segments de droite qui partagent un point commun appelé le sommet. Les angles peuvent être mesurés dans différentes unités, mais les unités les plus courantes sont les radians et les degrés.

Les radians sont une unité de mesure angulaire basée sur la longueur d'un arc d'un cercle. Un radian est défini comme l'angle qui sous-tend un arc de longueur égale au rayon du cercle. En d'autres termes, si un cercle a un rayon \(r\), alors un angle d'un radian au centre du cercle sous-tendra un arc de longueur \(r\). Le symbole des radians est "rad".

Les degrés sont une autre unité de mesure angulaire basée sur la division d'un cercle en 360 parties égales, chaque partie étant un degré. Le symbole des degrés est "\( \circ \)". Une révolution complète autour d'un cercle est équivalente à 360 degrés \( (360^\circ ) \).

Pour convertir entre radians et degrés, nous pouvons utiliser les formules suivantes:

• Pour convertir des radians en degrés: multiplier l'angle par \( \frac{180}{\pi} \).
• Pour convertir des degrés en radians: multiplier l'angle par \( \frac{\pi}{180} \).

Par exemple, supposons que nous ayons un angle de \( \theta = 2 \) radians. Pour convertir cet angle en degrés, nous pouvons utiliser la formule:
\( \theta = \text{radian} \cdot \frac{180}{\pi} = 2 \cdot \frac{180}{\pi} \approx 114.59^\circ \)

De même, supposons que nous ayons un angle de \( \theta = 45^\circ \). Pour convertir cet angle en radians, nous pouvons utiliser la formule:
\( \theta = \text{degrés} \cdot \frac{\pi}{180} = 45 \cdot \frac{\pi}{180} = \frac{\pi}{4} \approx 0.7854 \text{ rad} \)

En résumé, les radians et les degrés sont deux unités courantes de mesure angulaire utilisées pour mesurer les angles en géométrie. Les radians sont basés sur la longueur d'un arc d'un cercle, tandis que les degrés sont basés sur la division d'un cercle en 360 parties égales. Nous pouvons convertir entre radians et degrés en utilisant les formules mentionnées ci-dessus.

Fonctions trigonométriques et cercle unité ☰

Les fonctions trigonométriques sont des fonctions mathématiques qui relient les angles d'un triangle aux longueurs de ses côtés. Les fonctions trigonométriques les plus couramment utilisées sont le sinus, le cosinus et la tangente. Ces fonctions sont souvent représentées à l'aide du cercle unité, qui est un cercle de rayon 1 centré à l'origine d'un système de coordonnées cartésiennes.

Le cercle unité est utile car il nous permet de visualiser facilement les relations entre les angles et les fonctions trigonométriques. Si nous dessinons une ligne de l'origine à un point sur le cercle unité, l'angle entre cette ligne et l'axe x positif est appelé l'angle de rotation ou simplement l'angle. Le point où la ligne intersecte le cercle unité correspond à une valeur spécifique du sinus, du cosinus et de la tangente.

Voici les définitions des trois principales fonctions trigonométriques:

• Sinus (sin): le rapport de la longueur du côté opposé à l'angle à la longueur de l'hypoténuse d'un triangle rectangle.
• Cosinus (cos): le rapport de la longueur du côté adjacent à l'angle à la longueur de l'hypoténuse d'un triangle rectangle.
• Tangente (tan): le rapport de la longueur du côté opposé à l'angle à la longueur du côté adjacent à l'angle d'un triangle rectangle.

En utilisant le cercle unité, nous pouvons également définir les trois autres fonctions trigonométriques : cosécante (csc), sécante (sec) et cotangente (cot). Ce sont simplement les réciproques du sinus, du cosinus et de la tangente, respectivement.
Les fonctions sinus, tangente et cotangente sont impaires, et le cosinus est une fonction paire.

Fonctions trigonométriques de n'importe quel angle ☰

Les fonctions trigonométriques peuvent être définies pour n'importe quel angle, pas seulement pour les angles dans les triangles rectangles. Les définitions des fonctions trigonométriques d'un angle dans un cercle unité sont données ci-dessous:
Considérez un angle \(\theta\) en position standard, ce qui signifie qu'il commence à partir de l'axe \(x\) positif et tourne dans le sens antihoraire.
Soit \((x, y)\) le point où le côté terminal de l'angle \(\theta\) intersecte le cercle unité centré à l'origine.
Sinus (sin): \(sin(\theta) = y\)
Cosinus (cos): \(cos(\theta) = x\)
Tangente (tan): \(tan(\theta) = \frac{y}{x}\), \(x \neq 0\)

Les trois autres fonctions trigonométriques peuvent être définies comme suit:
Cosécante (csc): \(csc(\theta) = \frac{1}{sin \theta}\)
Sécan (sec): \(sec(\theta) = \frac{1}{cos \theta}\)
Cotangente (cot): \(cot(\theta) = \frac{1}{tan \theta}\)

Les valeurs des fonctions trigonométriques peuvent être positives, négatives ou nulles, selon le quadrant dans lequel l'angle \(\theta\) se trouve. Dans le premier quadrant \( ( 0 < \theta < 90 \text{ degrés}) \), les six fonctions trigonométriques sont positives. Dans le deuxième quadrant \( ( 90 < \theta < 180 \text{ degrés}) \), seul le sinus est positif. Dans le troisième quadrant \( ( 180 < \theta < 270 \text{ degrés}) \), seule la tangente est positive. Dans le quatrième quadrant \( ( 270 < \theta < 360 \text{ degrés}) \), seul le cosinus est positif.
Gardez à l'esprit que les angles peuvent être mesurés en degrés ou en radians. Les radians sont une autre façon de mesurer les angles, où un radian est défini comme l'angle qui sous-tend un arc de longueur égale au rayon du cercle. La conversion entre degrés et radians est donnée par:
\(\pi \text{ radians} = 180 \text{ degrés} \)
\( \text{1 radian } \approx 57.3 \text{ degrés} \)
\( \text{1 degré } \approx 0.0175 \text{ radians}\)

Lorsque vous travaillez avec les fonctions trigonométriques d'angles mesurés en radians, nous utilisons la lettre grecque \( \pi \) (pi) comme moyen pratique d'exprimer ces angles. Par exemple, un angle de 90 degrés peut être exprimé comme \( \frac{\pi}{2}\) radians, et un angle de 180 degrés peut être exprimé comme \( \pi \) radians.

Nous pouvons également utiliser des identités trigonométriques pour simplifier les expressions trigonométriques. Par exemple, l'identité trigonométrique de Pythagore stipule que \( sin^2 (\theta)+cos^2 (\theta)=1 \), ce qui est vrai pour toutes les valeurs de \( \theta \). Une autre identité utile est l'identité réciproque, qui relie les fonctions trigonométriques à leurs réciproques:

\( \csc(\theta) = \frac{1}{\sin(\theta)} \)
\( \sec(\theta) = \frac{1}{\cos(\theta)} \)
\( \cot(\theta) = \frac{1}{\tan(\theta)} \)

Il existe de nombreuses autres identités trigonométriques qui peuvent être utilisées pour simplifier les expressions trigonométriques ou résoudre des équations trigonométriques.
Dans l'ensemble, les fonctions trigonométriques de n'importe quel angle sont un concept important en mathématiques et ont une large gamme d'applications dans des domaines tels que la physique, l'ingénierie et la géométrie.

Formule de rotation ☰

Les formules de rotation sont un ensemble d'équations utilisées pour calculer les nouvelles coordonnées d'un point après qu'il ait été tourné d'un angle donné autour d'un point fixe dans un système de coordonnées. Il existe plusieurs variations de ces formules en fonction du problème spécifique, mais je vais expliquer l'idée de base derrière elles.

Supposons que nous ayons un point \(P\) dans le système de coordonnées, avec les coordonnées \((x, y)\). Nous voulons faire tourner ce point autour d'un point fixe \(O\) (appelé l'origine de la rotation) d'un angle de \( \theta \). Le but est de trouver les nouvelles coordonnées \((x', y')\) de \(P\) après cette rotation.
Pour ce faire, nous utilisons un ensemble d'équations qui relient les nouvelles coordonnées aux coordonnées originales et à l'angle de rotation. Une façon de dériver ces équations est d'utiliser la trigonométrie de base. Plus précisément, nous pouvons considérer le triangle formé par l'origine de la rotation \(O\), le point original \(P\) et le point tourné \(P'\). Les côtés de ce triangle ont des longueurs \(x\), \(y\) et \(r\) (la distance de \(O\) à \(P\)), et l'angle entre l'axe \(x\) et la ligne \(OP\) est \( \varphi \). Après la rotation, l'angle entre l'axe \(x\) et la ligne \(OP'\) est \( \varphi +\theta \).

En utilisant la trigonométrie, nous pouvons exprimer les nouvelles coordonnées \((x', y')\) en fonction des coordonnées originales \((x, y)\) et de l'angle de rotation \( \theta \) comme suit:
\( x' = xcos(\theta ) - ysin( \theta ) \)
\( y' = xsin(\theta ) + ycos(\theta ) \)
Ces équations nous donnent les nouvelles coordonnées de \(P'\) après avoir tourné \(P\) d'un angle \( \theta \) autour de \(O\).

Pour comprendre pourquoi ces équations fonctionnent, considérons la première équation. Le cosinus de \( \theta \) représente le changement de la coordonnée \(x\) de \(P\) après l'avoir tourné de \( \theta \), tandis que le sinus de \( \theta \) représente le changement de la coordonnée \(y\). Par conséquent, \( xcos( \theta ) \) représente la nouvelle coordonnée \(x\) de \(P'\) obtenue en tournant la coordonnée \(x\) originale de \(P\), et \(ysin(\theta ) \) représente la nouvelle coordonnée \(y\) obtenue en tournant la coordonnée \(y\) originale. En soustrayant ces quantités, nous obtenons la nouvelle coordonnée \(x\) de \(P'\) par rapport à l'axe \(x\). De même, la deuxième équation nous donne la nouvelle coordonnée \(y\) de \(P'\) par rapport à l'axe \(y\).

Il existe plusieurs variations des formules de rotation qui sont utilisées dans différents contextes. Voici quelques exemples:

Rotation autour d'un point autre que l'origine:
Les formules de rotation de base supposent que le point \(P\) est tourné autour de l'origine. Si nous voulons faire tourner le point autour d'un point différent \(Q\), nous pouvons d'abord translater le système de coordonnées de sorte que \(Q\) devienne l'origine, puis appliquer les formules de base, et enfin translater le système de coordonnées à nouveau. Alternativement, nous pouvons utiliser une forme plus générale des formules de rotation qui prend en compte les coordonnées du point \(Q\). Par exemple, si nous voulons faire tourner le point \(P\) d'un angle \( \theta \) autour du point \(Q\) avec les coordonnées \((a, b)\), les nouvelles coordonnées \((x', y')\) peuvent être calculées comme suit:
\( x' = (x-a) \cdot cos(\theta ) - (y-b) \cdot sin(\theta ) + a \)
\( y' = (x-a) \cdot sin(\theta ) + (y-b) \cdot cos(\theta ) + b \)

Rotation des nombres complexes:
En analyse complexe, un nombre complexe \(z\) peut être représenté comme \(z=x+yi\), où \(x\) et \(y\) sont les parties réelle et imaginaire, respectivement. Une rotation du plan complexe peut être représentée comme une multiplication du nombre complexe \(z\) par un nombre complexe de la forme \(w=cos(\theta )+isin(\theta ) \), où \( \theta \) est l'angle de rotation. Le nombre complexe résultant \(z'=wz\) a pour effet de faire tourner \(z\) dans le sens antihoraire autour de l'origine d'un angle de \( \theta\).

En résumé, les formules de rotation sont un outil fondamental en géométrie et en physique qui nous permettent de transformer des points et des objets en les faisant tourner autour d'un point ou d'un axe fixe. Elles peuvent être exprimées sous différentes formes en fonction du problème et sont utilisées dans une large gamme d'applications.

Les angles de rotation les plus courants sont \( 90^\circ \), \( 180^\circ \) et \(270^\circ \).

Remarque: dans le tableau, le point \((x,y)\) représente les coordonnées d'un point sur l'image originale avant la rotation, et le point dans la troisième colonne représente les coordonnées du même point après la rotation. L'angle de rotation est mesuré en degrés, et les directions "dans le sens des aiguilles d'une montre" et "dans le sens inverse des aiguilles d'une montre" se réfèrent à la direction de la rotation autour de l'origine.

Identités trigonométriques ☰

Les identités trigonométriques sont des équations mathématiques qui impliquent les fonctions trigonométriques (sinus, cosinus, tangente, etc.) et sont vraies pour toutes les valeurs possibles des variables impliquées. Ces identités sont largement utilisées en trigonométrie et en calcul pour simplifier et manipuler les expressions impliquant des fonctions trigonométriques.


Voici quelques-unes des identités trigonométriques les plus importantes:

Identité pythagoricienne:
\( \sin^2 (x) + \cos^2 (x) = 1 \)

Cette identité relie les fonctions sinus et cosinus et exprime le fait que la somme de leurs carrés est toujours égale à un. Elle est dérivée du théorème de Pythagore en géométrie, qui stipule que la somme des carrés des longueurs des côtés d'un triangle rectangle est égale au carré de la longueur de l'hypoténuse.

Identités réciproques:
\( \sin(x) = \frac{1}{\csc(x)} \)

\( \cos(x) = \frac{1}{\sec(x)} \)

\( \tan(x) = \frac{1}{\cot(x)} \)

Ces identités expriment les relations réciproques entre les fonctions trigonométriques et leurs fonctions réciproques correspondantes (cosécante, sécante et cotangente). Par exemple, la première identité stipule que le sinus d'un angle est égal à l'inverse de la cosécante de cet angle.

Identités pair-impair:
\( \sin(-x) = -\sin(x) \)
\( \cos(-x) = \cos(x) \)

Ces identités expriment la symétrie pair-impair des fonctions sinus et cosinus. Elles indiquent que la fonction sinus est une fonction impaire (c'est-à-dire qu'elle change de signe lorsque l'angle est négatif), tandis que la fonction cosinus est une fonction paire (c'est-à-dire qu'elle reste inchangée lorsque l'angle est négatif).

Identités de somme et de différence:
\( \sin(x+y) = \sin(x) \cos(y) + \cos(x)\sin(y) \)
\( \sin(x-y) = \sin(x) \cos(y) - \cos(x)\sin(y) \)
\( \cos(x+y) = \cos(x) \cos(y) - \sin(x)\sin(y) \)
\( \cos(x-y) = \cos(x) \cos(y) + \sin(x)\sin(y) \)

Ces identités expriment les fonctions trigonométriques de la somme et de la différence de deux angles en termes des fonctions trigonométriques des angles individuels. Elles sont largement utilisées en calcul et dans d'autres branches des mathématiques pour simplifier les expressions impliquant des fonctions trigonométriques.

Identités de double angle :
\( \sin (2x) = 2 \sin (x) \cos (x) \)

\( \cos(2x) = \cos^2 (x) - \sin^2 (x) = \) \(2\cos^2 (x) - 1 = 1-2 \sin^2 (x) \)

Ces identités expriment les fonctions trigonométriques du double d'un angle en termes des fonctions trigonométriques de l'angle lui-même. Elles sont largement utilisées en calcul et dans d'autres branches des mathématiques pour simplifier les expressions impliquant des fonctions trigonométriques.

Identités de demi-angle :
\( \sin( \frac{x}{2} ) = \pm \sqrt{ \frac{1- \cos x}{2} } \)

\( \cos( \frac{x}{2} ) = \pm \sqrt{ \frac{1+ \cos x}{2} } \)

\( \tan( \frac{x}{2} ) = \pm \sqrt{ \frac{1- \cos x}{1+ \cos x} } \)

Ces identités expriment les fonctions trigonométriques de la moitié d'un angle en termes des fonctions trigonométriques de l'angle lui-même. Elles sont largement utilisées en calcul et dans d'autres branches des mathématiques pour simplifier les expressions impliquant des fonctions trigonométriques.

Identités de produit à somme:
\( \sin(x)\sin(y) = \frac{1}{2} [\cos(x-y) - \cos(x+y) ] \)

\( \cos(x) \cos(y) = \frac{1}{2} [\cos(x-y) + \cos(x+y) ] \)

\( \sin(x) \cos(y) = \frac{1}{2} [\sin(x+y) + \sin(x-y) ] \)

Ces identités expriment le produit de deux fonctions trigonométriques comme une somme ou une différence de fonctions trigonométriques. Elles sont utilisées pour simplifier les produits impliquant des fonctions trigonométriques.

Identités de somme à produit:
\( \sin(x) + \sin(y) = 2 \sin [ \frac{x+y}{2} ] \cos [ \frac{x-y}{2} ] \)

\( \sin (x) - \sin (y) = 2 \cos [ \frac{x+y}{2} ] \sin [ \frac{x-y}{2} ] \)

\( \cos(x) + \cos(y) = 2 \cos[ \frac{x+y}{2} ] \cos[ \frac{x-y}{2} ] \)

\( \cos(x)-\cos(y) = -2\sin[ \frac{x+y}{2} ] \sin[ \frac{x-y}{2} ] \)

Ces identités expriment la somme ou la différence de deux fonctions trigonométriques comme un produit de fonctions trigonométriques. Elles sont utilisées pour simplifier les sommes ou les différences impliquant des fonctions trigonométriques.

Identités de cofonction :
\( \sin(x) = \cos( 90^\circ - x) \)
\( \cos(x) = \sin( 90^\circ - x) \)
\( \tan(x) = \text{ctg}( 90^\circ - x) \)
\( \text{ctg}(x) = \tan( 90^\circ - x) \)

Ces identités expriment la relation entre une fonction trigonométrique et sa cofonction (c'est-à-dire la fonction de l'angle complémentaire). Elles sont utilisées pour simplifier les expressions impliquant des angles complémentaires.

Identités de périodicité:
\( \sin(x + 2 \pi) = \sin(x) \)
\( \cos(x + 2 \pi ) = \cos(x) \)
\( \tan(x + \pi ) = \tan(x) \)

Ces identités expriment la nature périodique des fonctions trigonométriques. Elles indiquent que les fonctions sinus et cosinus se répètent tous les \(2 \pi \) radians, tandis que la fonction tangente se répète tous les \( \pi \) radians.

Ce sont quelques-unes des identités trigonométriques les plus importantes utilisées en mathématiques. En mémorisant ces identités et en comprenant comment les appliquer, les étudiants peuvent devenir compétents en trigonométrie et résoudre des problèmes difficiles impliquant des fonctions trigonométriques.

Simplifier les expressions trigonométriques ☰

Les fonctions trigonométriques sont une partie essentielle des mathématiques et de la physique, et simplifier les expressions trigonométriques est une compétence importante pour résoudre des équations et prouver des identités. Simplifier les expressions trigonométriques consiste à les manipuler algébriquement jusqu'à ce qu'elles soient dans une forme plus simple et plus facile à manipuler.

Les fonctions trigonométriques les plus courantes sont le sinus (sin), le cosinus (cos), la tangente (tan), la cotangente (cot), la sécante (sec) et la cosécante (csc). Ces fonctions peuvent être définies en termes des rapports des côtés d'un triangle rectangle ou comme des fonctions sur le cercle unité.

Pour simplifier une expression trigonométrique, il faut utiliser diverses identités et propriétés trigonométriques. Certaines des identités les plus couramment utilisées incluent:

Identités pythagoriciennes:
\( \sin^2(\theta) + \cos^2(\theta) = 1 \)
\( \tan^2(\theta) + 1 = \sec^2(\theta) \)
\( 1 + \cot^2(\theta) = \csc^2(\theta) \)

Identités de somme et de différence d'angles:
\( \sin(\alpha \pm \beta) = \sin(\alpha)\cos(\beta) \pm \cos(\alpha)\sin(\beta) \)
\( \cos(\alpha \pm \beta) = \cos(\alpha)\cos(\beta) \mp \sin(\alpha)\sin(\beta) \)
\( \tan(\alpha \pm \beta) = \frac{\tan(\alpha) \pm \tan(\beta)}{1 \mp \tan(\alpha)\tan(\beta)} \)

Identités de double angle:
\( \sin(2\theta) = 2\sin(\theta)\cos(\theta) \)
\( \cos(2\theta) = \cos^2(\theta) - \sin^2(\theta) \)
\( \tan(2\theta) = \frac{2\tan(\theta)}{1 - \tan^2(\theta)} \)

Identités de demi-angle:
\( \sin\left(\frac{\theta}{2}\right) = \pm\sqrt{\frac{1 - \cos(\theta)}{2}} \)
\( \cos\left(\frac{\theta}{2}\right) = \pm\sqrt{\frac{1 + \cos(\theta)}{2}} \)
\( \tan\left(\frac{\theta}{2}\right) = \pm\sqrt{\frac{1 - \cos(\theta)}{1 + \cos(\theta)}} \)

En utilisant ces identités, on peut simplifier une expression trigonométrique étape par étape jusqu'à ce qu'elle soit sous sa forme la plus simple. Quelques exemples de simplification d'expressions trigonométriques sont:

\( \sin^2 (x)+\cos^2 (x) \rightarrow 1 \)

\( \frac{\sin^2 (x)}{1-\cos(x)} \rightarrow \frac{1+\cos(x)}{2-\cos(x)} \)

\( \frac{\sin(x)}{\cos(x)} - \frac{\cos(x)}{\sin(x)} \rightarrow \frac{\sin^2 (x)-\cos^2 (x)}{\sin(x)\cos(x)} \)

\( \frac{\sin(x)}{\cos(x) +1} + \frac{1}{\cos(x)-1} \rightarrow \frac{2\sin(x)}{\cos^2 (x)-1} \)

Il est important de noter que lors de la simplification d'expressions trigonométriques, il faut faire attention au domaine de l'expression. Certaines fonctions trigonométriques ne sont pas définies pour certaines valeurs de l'angle, telles que \(tan(\theta)\) et \(cot(\theta)\) pour \( \theta = \frac{\pi}{2} +k \pi \) où \(k\) est un entier. De plus, certaines identités ne sont valides que pour certaines valeurs de l'angle ou lorsque certaines conditions sont remplies, comme les identités de demi-angle qui ne sont valides que pour \( \frac{\pi}{2} \le \theta \le \pi \) et \(cos(\theta) \le 0 \).

En résumé, simplifier les expressions trigonométriques consiste à utiliser diverses identités et propriétés pour les manipuler algébriquement jusqu'à ce qu'elles soient dans une forme plus simple. Il faut faire attention au domaine de l'expression et s'assurer que les identités utilisées sont valides pour les valeurs données de l'angle.