Angle of rotation ☰

The angle of rotation is a concept used in geometry to describe the amount of rotation applied to a figure around a fixed point called the center of rotation. When a figure is rotated, all points on the figure move along circular paths around the center of rotation, and the angle of rotation is the amount of rotation, measured in degrees or radians, that the figure undergoes.

To define the angle of rotation mathematically, we need to use the concept of the unit circle. The unit circle is a circle centered at the origin of the Cartesian plane with a radius of 1. We can use the unit circle to define the sine and cosine functions of an angle, which are fundamental trigonometric functions.

Suppose we have a point \((x,y) \) on the unit circle that makes an angle of \( \theta \) with the positive \(x\)-axis, as shown in the figure below:

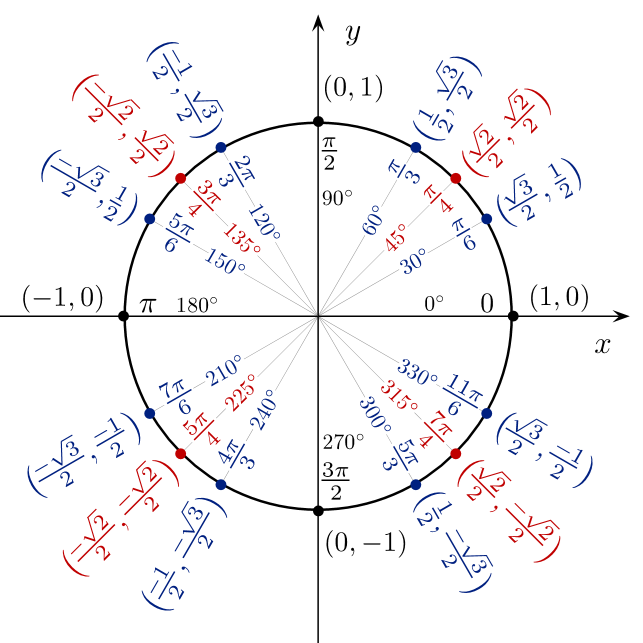
Then the coordinates of the point are given by:
\( x = cos( \theta ) \), \( y = sin( \theta) \).

The angle of rotation can be defined as follows. Suppose we have a figure \(F\) in the plane, and we rotate the figure counterclockwise around a fixed point \(O\) by an angle of \( \theta \). Let \(F' \) be the image of \(F\) under this rotation. Then the angle of rotation is defined as the angle between any two corresponding line segments of \(F \) and \(F' \) , both of which intersect at the center of rotation \(O\).
We can express the angle of rotation in terms of the coordinates of the points on the unit circle. Suppose we have a point \(P=(x,y) \) on \(F\) that rotates counterclockwise around \(O\) by an angle of \( \theta \), and let \(P'=(x',y' ) \) be the corresponding point on \(F' \). Then the angle of rotation can be calculated using the following formula:

\( \theta = \cos^{-1}\left(\frac{xx' + yy'}{\sqrt{x^2 + y^2} \sqrt{{x'}^2 + {y'}^2}}\right) \)

This formula is derived from the dot product formula for the angle between two vectors. The numerator of the fraction is the dot product of the vectors \(OP\) and \(OP'\), and the denominator is the product of their magnitudes.

In summary, the angle of rotation is a measure of the amount of rotation applied to a figure around a fixed point, and it can be calculated using the dot product formula or by measuring the angle between corresponding line segments of the original and rotated figures.

Degree and Radian Measure ☰

An angle is a geometric figure formed by two rays or line segments that share a common endpoint called the vertex. Angles can be measured in different units, but the most common units are radians and degrees.

Radians are a unit of angular measure that is based on the length of an arc of a circle. One radian is defined as the angle that subtends an arc of length equal to the radius of the circle. In other words, if a circle has a radius of r, then an angle of one radian at the center of the circle will subtend an arc of length \(r\). The symbol for radians is "rad".

Degrees are another unit of angular measure that is based on dividing a circle into 360 equal parts, each part being one degree. The symbol for degrees is "\( \circ \)". One full revolution around a circle is equivalent to 360 degrees \( (360^\circ ) \).

To convert between radians and degrees, we can use the following formulas:

• To convert from radians to degrees: multiply the angle by \( \frac{180}{\pi} \).
• To convert from degrees to radians: multiply the angle by \( \frac{\pi}{180} \).

For example, suppose we have an angle of \( \theta = 2 \text{ radians}\). To convert this angle to degrees, we can use the formula:
\( \theta = \text{radian} \cdot \frac{180}{\pi} = 2 \cdot \frac{180}{\pi} \approx 114.59^\circ \)

Similarly, suppose we have an angle of \( \theta = 45^\circ \). To convert this angle to radians, we can use the formula:
\( \theta = \text{degrees} \cdot \frac{\pi}{180} = 45 \cdot \frac{\pi}{180} = \frac{\pi}{4} \approx 0.7854 \text{ rad} \)

In summary, radians and degrees are two common units of angular measure used to measure angles in geometry. Radians are based on the length of an arc of a circle, while degrees are based on dividing a circle into 360 equal parts. We can convert between radians and degrees using the formulas mentioned above.

Trigonometric Functions and the Unit Circle ☰

Trigonometric functions are mathematical functions that relate the angles of a triangle to the lengths of its sides. The most commonly used trigonometric functions are sine, cosine, and tangent. These functions are often represented using the unit circle, which is a circle with a radius of 1 centered at the origin of a Cartesian coordinate system.

The unit circle is useful because it allows us to easily visualize the relationships between angles and trigonometric functions. If we draw a line from the origin to a point on the unit circle, the angle between that line and the positive x-axis is known as the angle of rotation or simply the angle. The point where the line intersects the unit circle corresponds to a specific value of sine, cosine, and tangent.

Here are the definitions of the three main trigonometric functions:

• Sine (sin): the ratio of the length of the side opposite the angle to the length of the hypotenuse of a right triangle.
• Cosinus (cos): the ratio of the length of the side adjacent to the angle to the length of the hypotenuse of a right triangle.
• Tangents (tan): the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle of a right triangle.

Using the unit circle, we can also define the other three trigonometric functions: cosecant (csc), secant (sec), and cotangent (cot). These are simply the reciprocals of sine, cosine, and tangent, respectively.
Sine, tangent, cotangent functions are odd, and cosine is an even function.

Trigonometric functions of any angle ☰

Trigonometric functions can be defined for any angle, not just angles in right triangles. The definitions of the trigonometric functions of an angle in a unit circle are given below:
Consider an angle \(\theta \) in standard position, meaning it starts from the positive \(x\)-axis and rotates counterclockwise.
Let \((x,y)\) be the point where the terminal side of the angle \( \theta \) intersects the unit circle centered at the origin.
Sine (sin): \( sin(\theta ) = y \)
Cosinus (cos): \( cos( \theta ) = x \)
Tangent (tan): \( tan( \theta ) = \frac{y}{x} \), \(x \neq 0 \)

The other three trigonometric functions can be defined as follows:
Cosecant (csc): \( csc( \theta ) = \frac{1}{sin \theta } \)
Secant (sec): \( sec(\theta ) = \frac{1}{cos \theta } \)
Cotangent (cot): \( cot(\theta ) = \frac{1}{tan \theta } \)

The values of the trigonometric functions can be positive, negative, or zero, depending on the quadrant in which the angle \( \theta \) lies. In the first quadrant \( ( 0 < \theta < 90 \text{ degrees}) \), all six trigonometric functions are positive. In the second quadrant \( ( 90 < \theta < 180 \text{ degrees}) \), only sine is positive. In the third quadrant \( ( 180 < \theta < 270 \text{ degrees}) \), only tangent is positive. In the fourth quadrant \( ( 270 < \theta < 360 \text{ degrees}) \), only cosine is positive.
Keep in mind that the angles can be measured in degrees or radians. Radians are another way to measure angles, where one radian is defined as the angle that subtends an arc of length equal to the radius of the circle. The conversion between degrees and radians is given by:
\(\pi \text{ radians} = 180 \text{ degrees} \)
\( \text{1 radians } \approx 57.3 \text{ degrees} \)
\( \text{1 degrees } \approx 0.0175 \text{ radians} \)

When working with trigonometric functions of angles measured in radians, we use the Greek letter \( \pi \) (pi) as a convenient way to express these angles. For example, an angle of 90 degrees can be expressed as \( \frac{\pi}{2}\) radians, and an angle of 180 degrees can be expressed as \( \pi \) radians.

We can also use trigonometric identities to simplify trigonometric expressions. For example, the Pythagorean identity states that \( sin^2 (\theta)+cos^2 (\theta)=1 \), which is true for all values of \( \theta \). Another useful identity is the reciprocal identity, which relates the trigonometric functions to their reciprocals:

\( \csc(\theta) = \frac{1}{\sin(\theta)} \)
\( \sec(\theta) = \frac{1}{\cos(\theta)} \)
\( \cot(\theta) = \frac{1}{\tan(\theta)} \)

There are many other trigonometric identities that can be used to simplify trigonometric expressions or solve trigonometric equations.
Overall, trigonometric functions of any angle are an important concept in mathematics and have a wide range of applications in fields such as physics, engineering, and geometry.

Rotation formula ☰

The rotation formulas are a set of equations used to calculate the new coordinates of a point after it has been rotated by a given angle about a fixed point in a coordinate system. There are several variations of these formulas depending on the specific problem, but I will explain the basic idea behind them.

Suppose we have a point \(P\) in the coordinate system, with coordinates \((x,y)\). We want to rotate this point about a fixed point \(O\) (called the origin of rotation) by an angle of \( \theta \) . The goal is to find the new coordinates \((x',y' ) \) of \(P\) after this rotation.
To do this, we use a set of equations that relate the new coordinates to the original coordinates and the rotation angle. One way to derive these equations is to use basic trigonometry. Specifically, we can consider the triangle formed by the origin of rotation \(O\), the original point \(P\), and the rotated point \(P'\). The sides of this triangle have lengths \(x\), \(y\), and \(r\) (the distance from O to P), and the angle between the \(x\)-axis and the line \(OP\) is \( \varphi \). After the rotation, the angle between the \(x\)-axis and the line \(OP'\) is \( \varphi +\theta \).

Using trigonometry, we can express the new coordinates \((x',y' ) \) in terms of the original coordinates \((x,y)\) and the rotation angle \(\theta \) as follows:
\( x' = xcos(\theta ) - ysin( \theta ) \)
\( y' = xsin( \theta ) + ycos( \theta ) \)
These equations give us the new coordinates of \(P'\) after rotating \(P\) by an angle \( \theta \) about \(O\).

To understand why these equations work, consider the first equation. The cosine of \(\theta \) represents the change in the \(x\)-coordinate of \(P\) after rotating it by \( \theta \) , while the sine of \( \theta \) represents the change in the \(y\)-coordinate. Therefore, \( xcos( \theta ) \) represents the new \(x\)-coordinate of \(P'\) obtained by rotating the original \(x\)-coordinate of \(P\), and \(ysin(\theta ) \) represents the new \(y\)-coordinate obtained by rotating the original \(y\)-coordinate. Subtracting these quantities gives us the new \(x\)-coordinate of \(P'\) relative to the \(x\)-axis. Similarly, the second equation gives us the new \(y\)-coordinate of \(P'\) relative to the \(y\)-axis.

There are several variations of the rotation formulas that are used in different contexts. Here are some examples:

Rotating about a point other than the origin:
The basic rotation formulas assume that the point \(P\) is being rotated about the origin. If we want to rotate the point about a different point \(Q\), we can first translate the coordinate system so that \(Q\) becomes the origin, then apply the basic formulas, and finally translate the coordinate system back. Alternatively, we can use a more general form of the rotation formulas that takes into account the coordinates of the point \(Q\). For example, if we want to rotate the point \(P\) by an angle \( \theta \) about the point \(Q\) with coordinates \((a,b)\), the new coordinates \((x',y') \) can be computed as follows:
\( x' = (x-a) \cdot cos(\theta ) - (y-b) \cdot sin(\theta ) + a \)
\( y' = (x-a) \cdot sin(\theta ) + (y-b) \cdot cos(\cdot ) + b \)

Rotating complex numbers:
In complex analysis, a complex number \(z\) can be represented as \(z=x+yi\), where \(x\) and \(y\) are the real and imaginary parts, respectively. A rotation of the complex plane can be represented as a multiplication of the complex number \(z\) by a complex number of the form \(w=cos(\theta )+isin(\theta ) \), where \(\theta \) is the angle of rotation. The resulting complex number \(z'=wz\) has the effect of rotating \(z\) counterclockwise about the origin by an angle of \(\theta\).

In summary, the rotation formulas are a fundamental tool in geometry and physics that allow us to transform points and objects by rotating them about a fixed point or axis. They can be expressed in various forms depending on the problem, and are used in a wide range of applications.

The most common rotation angles are \( 90^\circ \), \( 180^\circ \) and \(270^\circ \).

Note that in the table, the point \((x,y) \) represents the coordinates of a point on the original image before rotation, and the point in the third column represents the coordinates of the same point after rotation. The angle of rotation is measured in degrees, and the directions "clockwise" and "counterclockwise" refer to the direction of rotation around the origin.

Trigonometric Identities ☰

Trigonometric identities are mathematical equations that involve the trigonometric functions (sine, cosine, tangent, etc.) and are true for all possible values of the variables involved. These identities are used extensively in trigonometry and calculus to simplify and manipulate expressions involving trigonometric functions.


Here are some of the most important trigonometric identities:

Pythagorean identity:
\( sin^2 (x) + cos^2 (x) = 1 \)

This identity relates the sine and cosine functions and expresses the fact that the sum of their squares is always equal to one. It is derived from the Pythagorean theorem in geometry, which states that the sum of the squares of the lengths of the legs of a right triangle is equal to the square of the length of the hypotenuse.

Reciprocal identities:
\( sin(x) = \frac{1}{csc(x)} \)

\( cos(x) = \frac{1}{sec(x)} \)

\( tan(x) = \frac{1}{cot(x)} \)

These identities express the reciprocal relationships between the trigonometric functions and their corresponding reciprocal functions (cosecant, secant, and cotangent). For example, the first identity states that the sine of an angle is equal to the reciprocal of the cosecant of that angle.

Even-odd identities:
\( sin(-x) = -sin(x) \)
\( cos(-x) = cos(x) \)

These identities express the even-odd symmetry of the sine and cosine functions. They state that the sine function is an odd function (i.e., it changes sign when the angle is negated), while the cosine function is an even function (i.e., it remains unchanged when the angle is negated).

Sum and difference identities:
\( sin(x+y) = sin(x) cos(y) + cos(x)sin(y) \)
\( sin(x-y) = sin(x) cos(y) - cos(x)sin(y) \)
\( cos(x+y) = cos(x) cos(y) - sin(x)sin(y) \)
\( cos(x-y) = cos(x) cos(y) + sin(x)sin(y) \)

These identities express the trigonometric functions of the sum and difference of two angles in terms of the trigonometric functions of the individual angles. They are used extensively in calculus and other branches of mathematics to simplify expressions involving trigonometric functions.

Double angle identities:
\( sin (2x) = 2 sin (x) cos (x) \)

\( cos(2x) = cos^2 (x) - sin^2 (x) = \) \(2cos^2 (x) - 1 = 1-2 sin^2 (x) \)

These identities express the trigonometric functions of twice an angle in terms of the trigonometric functions of the angle itself. They are used extensively in calculus and other branches of mathematics to simplify expressions involving trigonometric functions.

Half angle identities:
\( sin( \frac{x}{2} ) = \pm \sqrt{ \frac{1- cos x}{2} } \)

\( cos( \frac{x}{2} ) = \pm \sqrt{ \frac{1+ cos x}{2} } \)

\( tan( \frac{x}{2} ) = \pm \sqrt{ \frac{1- cos x}{1+ cos x} } \)

These identities express the trigonometric functions of half an angle in terms of the trigonometric functions of the angle itself. They are used extensively in calculus and other branches of mathematics to simplify expressions involving trigonometric functions.

Product-to-sum identities:
\( sin(x)sin(y) = \frac{1}{2} [cos(x-y) - cos(x+y) ] \)

\( cos(x) cos(y) = \frac{1}{2} [cos(x-y) + cos(x+y) ] \)

\( sin(x) cos(y) = \frac{1}{2} [sin(x+y) + sin(x-y) ] \)

These identities express the product of two trigonometric functions as a sum or difference of trigonometric functions. They are used to simplify products involving trigonometric functions.

Sum-to-product identities:
\( sin(x) + sin(y) = 2 sin [ \frac{x+y}{2} ] cos [ \frac{x-y}{2} ] \)

\( sin (x) - sin (y) = 2 cos [ \frac{x+y}{2} ] sin [ \frac{x-y}{2} ] \)

\( cos(x) + cos(y) = 2 cos[ \frac{x+y}{2} ] cos[ \frac{x-y}{2} ] \)

\( cos(x)-cos(y) = -2sin[ \frac{x+y}{2} ] sin[ \frac{x-y}{2} ] \)

These identities express the sum or difference of two trigonometric functions as a product of trigonometric functions. They are used to simplify sums or differences involving trigonometric functions.

Cofunction identities:
\( sin(x) = cos( 90^\circ - x) \)
\( cos(x) = sin( 90^\circ - x) \)
\( tan(x) = ctg( 90^\circ - x) \)
\( ctg(x) = tan( 90^\circ - x) \)

These identities express the relationship between a trigonometric function and its cofunction (i.e., the function of the complementary angle). They are used to simplify expressions involving complementary angles.

Periodicity identities:
\( sin(x + 2 \pi) = sin(x) \)
\( cos(x + 2 \pi ) = cos(x) \)
\( tan(x + \pi ) = tan(x) \)

These identities express the periodic nature of the trigonometric functions. They state that the sine and cosine functions repeat themselves every \(2 \pi \) radians, while the tangent function repeats itself every \( \pi \) radians.

These are some of the most important trigonometric identities that are used in mathematics. By memorizing these identities and understanding how to apply them, students can become proficient in trigonometry and solve challenging problems involving trigonometric functions.

Simplifying trigonometric expressions ☰

Trigonometric functions are an essential part of mathematics and physics, and simplifying trigonometric expressions is an important skill for solving equations and proving identities. Simplifying trigonometric expressions involves manipulating them algebraically until they are in a simpler form that is easier to work with.

The most common trigonometric functions are the sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (csc). These functions can be defined in terms of the ratios of the sides of a right triangle, or as functions on the unit circle.

To simplify a trigonometric expression, one must use various trigonometric identities and properties. Some of the most commonly used identities include:

Pythagorean identities:
\( \sin^2(\theta) + \cos^2(\theta) = 1 \)
\( \tan^2(\theta) + 1 = \sec^2(\theta) \)
\( 1 + \cot^2(\theta) = \csc^2(\theta) \)

Angle Sum and Difference Identities:
\( \sin(\alpha \pm \beta) = \sin(\alpha)\cos(\beta) \pm \cos(\alpha)\sin(\beta) \)
\( \cos(\alpha \pm \beta) = \cos(\alpha)\cos(\beta) \mp \sin(\alpha)\sin(\beta) \)
\( \tan(\alpha \pm \beta) = \frac{\tan(\alpha) \pm \tan(\beta)}{1 \mp \tan(\alpha)\tan(\beta)} \)

Double Angle Identities:
\( \sin(2\theta) = 2\sin(\theta)\cos(\theta) \)
\( \cos(2\theta) = \cos^2(\theta) - \sin^2(\theta) \)
\( \tan(2\theta) = \frac{2\tan(\theta)}{1 - \tan^2(\theta)} \)

Half Angle Identities:
\( \sin\left(\frac{\theta}{2}\right) = \pm\sqrt{\frac{1 - \cos(\theta)}{2}} \)
\( \cos\left(\frac{\theta}{2}\right) = \pm\sqrt{\frac{1 + \cos(\theta)}{2}} \)
\( \tan\left(\frac{\theta}{2}\right) = \pm\sqrt{\frac{1 - \cos(\theta)}{1 + \cos(\theta)}} \)

Using these identities, one can simplify a trigonometric expression step by step until it is in its simplest form. Some examples of simplifying trigonometric expressions are:

\( sin^2 (x)+cos^2 (x) \rightarrow 1 \)

\( \frac{sin^2 (x)}{1-cos(x)} \rightarrow \frac{1+cos(x)}{2-cos(x)} \)

\( \frac{sin(x)}{cos(x)} - \frac{cos(x)}{sin(x)} \rightarrow \frac{sin^2 (x)-cos^2 (x)}{sin(x)cos(x)} \)

\( \frac{sin(x)}{cos(x) +1} + \frac{1}{cos(x)-1} \rightarrow \frac{2sin(x)}{cos^2 (x)-1} \)

It is important to note that when simplifying trigonometric expressions, one should pay attention to the domain of the expression. Some trigonometric functions are not defined for certain values of the angle, such as \(tan(\theta )\) and \(cot(\theta ) \) for \( \theta = \frac{\pi}{2} +k \pi \) where \(k\) is an integer. In addition, some identities are only valid for certain values of the angle or when certain conditions are met, such as the half angle identities only being valid for \( \frac{\pi}{2} \le \theta \le \pi \) and \(cos(\theta ) \le 0 \).

In summary, simplifying trigonometric expressions involves using various identities and properties to manipulate them algebraically until they are in a simpler form. One must pay attention to the domain of the expression and ensure that the identities used are valid for the given values of the angle.