Dövri funksiyalar. Triqonometrik funksiyaların dövriliyi. ☰

Tutaq ki, elə \( T \neq 0 \) ədədi var ki, funksiyanın təyin oblastından götürülmüş istənilən \(x\) üçün \( x \pm T \)-də təyin oblastına daxildir və \( f(x-T)=f(x)=f(x+T) \) ödənir. Onda f(x) funksiyasına dövrü T olan dövri funksiya deyilir. Funksiyanın ən kiçik müsbət dövrünə onun əsas dövrü deyilir.

• "T" ədədi "f" funksiyasının dövrüdürsə "(-T)" ədədi də "f" funksiyasının dövrü olur.
• \( T_1 \) və “\( T_2 \)” ədədləri f funksiyasının dövrüdürsə \( T_1 + T_2 \) və \( T_1 - T_2 \) ədədləri də f funksiyasının dövrü olur.
• T ədədi f funksiyasının dövrüdürsə, n istənilən tam ədəd olduqda "nT" ədədi də f funksiyasının dövrüdür.
  \( y = f(x) \) funksiyası dövridirsə, onun dövrlərinin sayı sonsuzdur. Buradan da dediklərimizi ümumiləşdirsək,
  \(f(x) = f(x+T) = f(x+2T) = \) \( f(x+3T) = ⋯ = f(x+nT) = ⋯ \) alınacaq.
• \( y = f(x) \) dövri funksiyadırsa, onun təyin oblastı koordinat başlanğıcına nəzərən simmetrikdir və sonsuz çoxluqdur.

Sinus və kosinus kimi triqonometrik funksiyalar dövri funksiyaların əsas nümunələridir. Sinus və kosinus funksiyalarının dövriliyini müzakirə edək:

Sinus funksiyası: \(sin(x) \) ilə işarələnən sinus funksiyası \( 2 \pi \) periyodu ilə dövri xarakter daşıyır. Bu o deməkdir ki, bütün \(x\)-lar üçün:
\( sin ( x + 2 \pi ) = sin(x) \)
Başqa sözlə, sinus funksiyası öz dəyərlərini \(x\) oxu boyunca hər \(2 \pi \) vahidindən bir təkrarlayır.

Kosinus funksiyası: \(cos(x) \) ilə işarələnən kosinus funksiyası da \( 2 \pi \) periyodu ilə dövri xarakter daşıyır. Bu o deməkdir ki, bütün \(x\)-lar üçün:
\( cos (x + 2 \pi ) = cos(x) \)

Sinus funksiyası kimi, kosinus funksiyası da öz dəyərlərini \(x\) oxu boyunca hər \( 2 \pi \) vahiddən bir təkrarlayır.
\( tan(x) \) ilə işarələnən tangens funksiyası dövri triqonometrik funksiyanın başqa bir nümunəsidir. Lakin onun dövrü sinus və kosinus funksiyalarından fərqlidir. Tangens funksiyasının \( \pi \) dövrü var, bu o deməkdir ki, bütün \(x\)-lar üçün:
\( tg(x+ \pi ) = tg(x) \)

Tangens funksiyası öz dəyərlərini \(x\) oxu boyunca hər \( \pi \) vahidində təkrarlayır.

Sinus (y=sin(x)) və kosinus (y=cos(x)) funksiyalarının qrafikləri ☰

Sinus və kosinus funksiyalarının \( (y=sin(x) \text{ və } y=cos(x)) \) qrafikləri onların xassələrini və davranışlarını anlamaq üçün vacibdir. Hər iki funksiya dövridir və -1 ilə 1 arasında dalğalanır. Qrafiklər bu funksiyaların dövriliyini və amplitudasını nümayiş etdirir. Hər iki funksiyanın qrafiklərini ətraflı müzakirə edək.

\( y=sin(x) \) funksiyasının qrafiki:
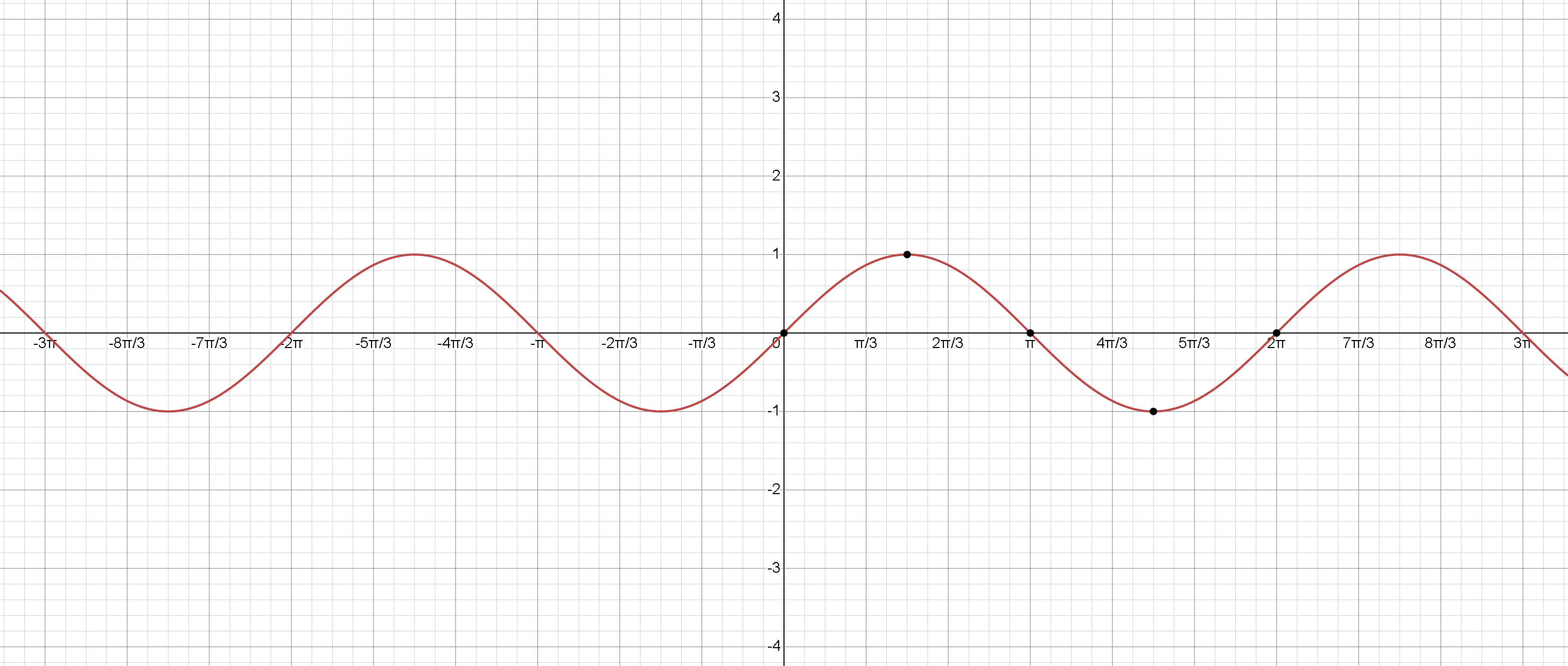
Sinus funksiyasının \( 2 \pi \) dövrü var. Bu o deməkdir ki, o, öz dəyərlərini \(x\) oxu boyunca hər \(2 \pi \) vahiddən bir təkrarlayır. Sinus funksiyasının qrafiki koordinat başlanğıcından \((0,0)\) başlayır və -1 ilə 1 arasında dalğalanır:
\( x = \frac{ \pi }{2} \), \( sin(x)=1 \) (maksimum qiyməti)
\( x = \pi \), \( sin(x) = 0 \) (sıfır nöqtəsi)
\( x= \frac{3 \pi }{2} \), \( sin(x)= -1 \) (minimum qiyməti)
\(x=2 \pi \), \( sin(x)=0 \) (bir tam dövrdəki sıfır nöqtəsi)

Sinus funksiyası dalğavari formaya malikdir və onun qrafiki koordinat başlanğıcına görə simmetrikdir (tək funksiyadır). Qrafik həm müsbət, həm də mənfi \(x\) istiqamətlərində sonsuz şəkildə uzanır və hər \(2 \pi \) vahidində özünü təkrarlayır.


\( \mathbf{ y=cos(x) } \) funksiyasının qrafiki:
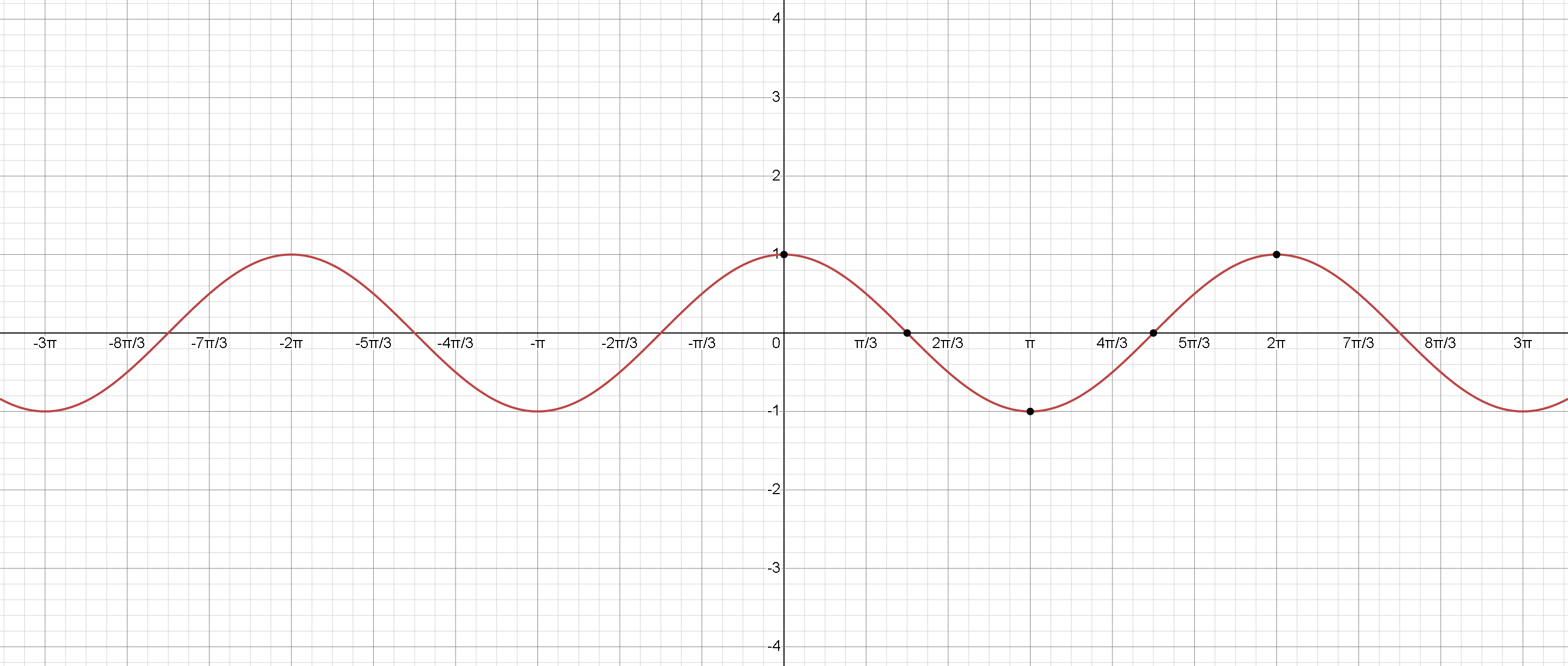
Kosinus funksiyası, sinus funksiyası kimi, \( 2 \pi \) dövrünə malikdir və -1 ilə 1 arasında dalğalanır. Bununla belə, kosinus funksiyasının qrafiki sinus funksiyası ilə müqayisədə faza olaraq \( \frac{ \pi }{2} \) vahid sola sürüşür. Kosinus funksiyası üçün bəzi əsas məqamlar bunlardır:
\( x =0 \), \( cos(x)=1 \) (maksimum qiyməti)
\( x = \frac{ \pi }{2} \), \( cos(x)=0 \) (sıfır nöqtəsi)
\( x = \pi \), \( cos(x)= -1 \) (minimum qiyməti)
\( x= \frac{3 \pi }{2} \), \( cos(x)=0 \) (sıfır nöqtəsi)
\(x = 2 \pi \), \( cos(x)= 1\) (bir tam dövrdəki sıfır nöqtəsi)

Kosinus funksiyası da dalğavari formaya malikdir və onun qrafiki y oxuna görə simmetrikdir. Qrafik həm müsbət, həm də mənfi \(x\) istiqamətlərində sonsuz şəkildə uzanır və hər \( 2 \pi \) vahidində özünü təkrarlayır.

Sinus və kosinus funksiyalarının qrafiklərinin çevrilməsi ☰

Sinus və kosinus funksiyalarının transformasiyası amplituda, dövr, faza sürüşməsi və şaquli yerdəyişmə kimi müxtəlif xüsusiyyətlərə malik yeni funksiyalar yaratmaq üçün əsas sinus və kosinus funksiyalarının dəyişdirilməsini nəzərdə tutur. Bu transformasiyalar bizə fizika, mühəndislik və musiqi kimi müxtəlif sahələrdə dövri hadisələrin geniş spektrini modelləşdirməyə imkan verir. Əsas sinus və kosinus funksiyaları aşağıdakılarla verilir:
\( f(x) = sin(x) \)
\( g(x) = cos(x) \)

Dörd ümumi çevrilmənin qısa izahı bunlardır:
Amplituda: Amplituda funksiyanın pik dəyəri və ya funksiyanın mərkəzi oxundan maksimum məsafəsidir. Amplitudanın dəyişdirilməsi sinus və ya kosinus funksiyasının "A" ilə işarələnən sabitə vurulmasını nəzərdə tutur:
\( f(x)= Asin(x) \)
\( g(x) = Acos(x) \)
\( A > 1 \) olarsa, amplituda artır, \( 0 < A < 1 \) olarsa, amplituda azalır. \(A\) mənfi olarsa, funksiya üfüqi \(ox\) üzərində əks olunur.

Period: Dövr, funksiyanın təkrarlandığı intervaldır. Sinus və ya kosinus funksiyasının dövrünü dəyişdirmək üçün giriş dəyişənini "B" ilə işarələnən sabitə vururuq:
\( f(x) = sin(Bx) \)
\( g(x) = cos(Bx) \)
Funksiyanın yeni dövrü, ilkin dövrü (həm sinus, həm də kosinus funksiyaları üçün \( 2 \pi \) ) \(B\)-nin mütləq qiymətinə bölmək yolu ilə tapılır:
\( \text{Yeni dövr } = \frac{2 \pi }{ |B| } \). \( B > 1 \) olarsa, funksiya üfüqi olaraq sıxılır, \( 0 < B < 1 \) olarsa, funksiya üfüqi olaraq dartılır.

Üfüqi sürüşmə (faza): Faza sürüşməsi funksiyanın üfüqi yerdəyişməsidir. Bu, giriş dəyişənindən "C" ilə işarələnən sabiti əlavə etmək və ya çıxmaqla əldə edilir:
\( f(x) = sin( B \cdot (x-C) ) \)
\( g(x) = cos ( B \cdot (x-C) ) \)
Fazanın müsbət yerdəyişməsi (\(C > 0 \) ) funksiyanı sağa, mənfi faza sürüşməsi (\( C < 0 \) ) isə funksiyanı sola aparır.

Şaquli sürüşmə: Şaquli yerdəyişmə bütün funksiyaya "D" ilə işarələnən sabiti əlavə etmək və ya çıxmaqla funksiyanı yuxarı və ya aşağı hərəkət etdirir:
\( f(x) = Asin(B(x - C)) + D \)
\( g(x) = Acos(B(x - C)) + D \)
Müsbət şaquli sürüşmə \( ( D > 0 ) \) funksiyanı yuxarıya, mənfi şaquli sürüşmə \(( D < 0 ) \) isə aşağıya doğru sürüşdürür.

Xülasə, sinus və kosinus funksiyalarının çevrilməsi müxtəlif dövri hadisələri modelləşdirmək üçün onların amplitudasının, dövrünün, faza sürüşməsinin və şaquli yerdəyişmənin dəyişdirilməsini əhatə edir. Ümumi çevrilmiş sinus və kosinus funksiyaları aşağıdakı kimi yazıla bilər:
\( f(x) = Asin(B(x-C))+D \)
\( g(x) = Acos(B(x-C))+D \)
Sinus və kosinus funksiyalarının çevrilmələrini araşdırmağa davam etmək üçün bu çevrilmələrin bəzi nümunələrinə və tətbiqlərinə baxaq.

Nümunə 1: Siqnal emalı
Siqnal emalında amplituda modulyasiyası (\(AM\)) davamlı dalğa siqnalının amplitudasını dəyişdirərək məlumat ötürmək üçün istifadə olunan bir texnikadır. Modulyasiya daşıyıcı dalğa və mesaj siqnalının hasili ilə təmsil oluna bilər:
\( y(t)= (A + Msin(Bmt)) \cdot cos(Bc\cdot t) \)
Burada, \(A\) daşıyıcı dalğanın amplitudasını, \(Bc\) daşıyıcı dalğanın bucaq tezliyini, \(M\) mesaj siqnalının amplitudasını, \(Bm\) mesaj siqnalının bucaq tezliyini, \(t\) isə zaman dəyişənini ifadə edir. Transformasiya yüksək tezlikli daşıyıcı dalğanın aşağı tezlikli mesaj siqnalı ilə birləşməsinə imkan verir.

Nümunə 2: Fizika - Sadə Harmonik Hərəkət
Fizikada sadə harmonik hərəkət (SHM) yay və ya sarkaçla bağlanmış kütlə kimi hərəkət edən cismin hərəkətini təsvir edir. Cismin tarazlıq mövqeyindən zamana görə yerdəyişməsi sinus və ya kosinus funksiyasından istifadə etməklə modelləşdirilə bilər:
\( x(t) = A\cos(\omega t + \varphi) \)
Burada \(A\) - hərəkətin amplitudası, \( \omega \) - bucaq tezliyi, \(t\) - vaxt, \( \varphi \) - faza bucağı. Faza bucağı cismin ilkin mövqeyini \( t = 0 \)-da müəyyən edir. Sadə harmonik hərəkət çevrilmiş sinus və kosinus funksiyalarından istifadə etməklə təhlil edilə və proqnozlaşdırıla bilər.

Nümunə 3: Səs və Musiqi
Akustikada səs dalğaları sinus və kosinus funksiyalarından istifadə edərək modelləşdirilə bilər. Saf tonun dalğa forması aşağıdakı kimi təqdim edilə bilər:
\( y(t) = Asin(2 \pi f \cdot t + \varphi ) \)
Burada, \(A\) səs dalğasının amplitudasıdır ki, bu da səsin ucalığını təyin edir; \(f\) - səsin hündürlüyünü təyin edən səs dalğasının tezliyi; \(t\) zaman dəyişəni, \( \varphi \) isə dalğanın ilkin mövqeyini təyin edən faza bucağıdır. Sinus və kosinus funksiyalarını çevirməklə biz mürəkkəb səsləri və musiqini təhlil edib sintez edə bilərik.

Bu nümunələr müxtəlif sahələrdə çevrilmiş sinus və kosinus funksiyalarının çox yönlülüyünü göstərir. Amplituda, dövr, faza sürüşməsi və şaquli yerdəyişməni tənzimləməklə biz çoxlu dövri hadisələri modelləşdirə və müxtəlif fənlər üzrə problemləri həll edə bilərik.

Tangens və kotangens funksiyalarının qrafikləri ☰

Tangens və kotangens sinus və kosinus funksiyaları ilə əlaqəli triqonometrik funksiyalardır. Onlar dövri xarakter daşıyır və onları öyrənmək üçün maraqlı edən unikal xüsusiyyətlər nümayiş etdirirlər. Bu iki funksiyanın qrafiklərinə dərindən nəzər salaq:

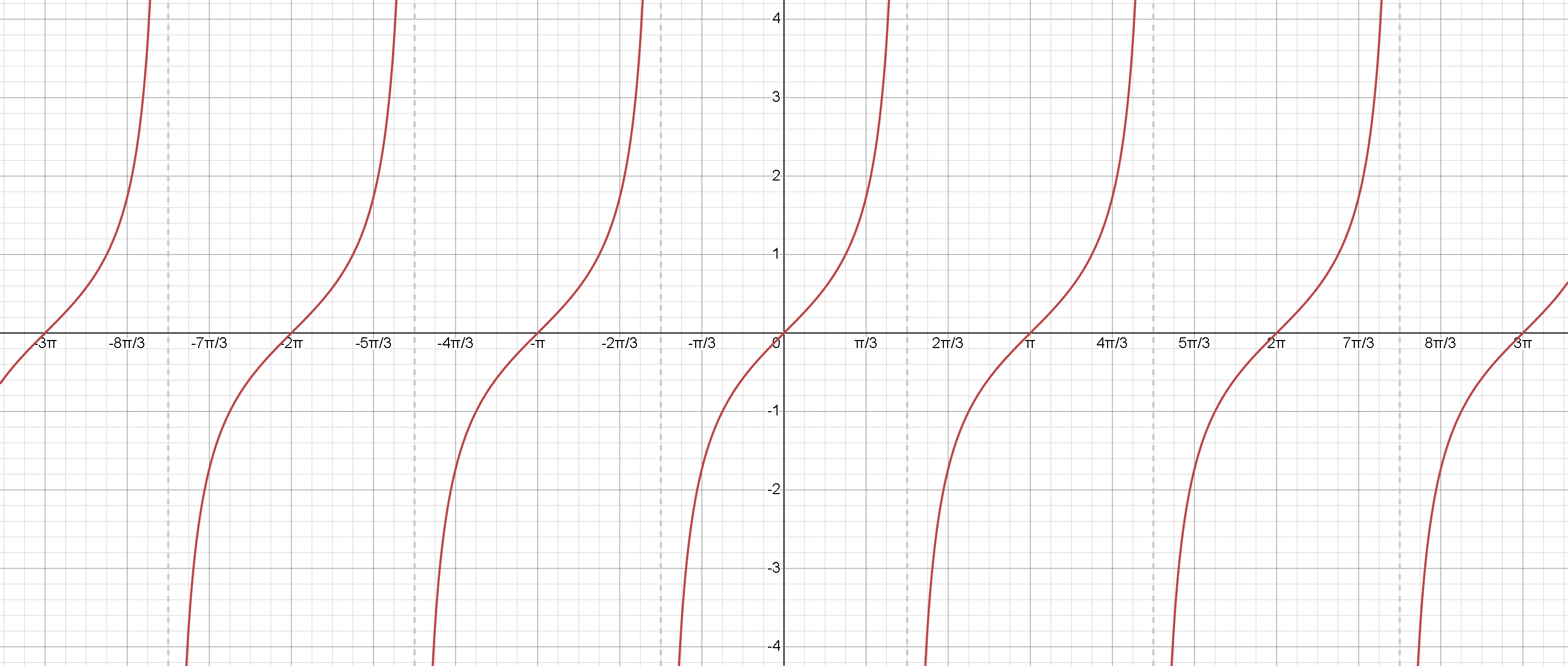
1. Tangens Funksiyası \( tg(x) \):
Tangens funksiyası sinus funksiyasının kosinus funksiyasına nisbəti kimi müəyyən edilir.
\( tg(x) = \frac{sin(x)}{cos(x)} \)

Tangens qrafikinin əsas xüsusiyyətləri:

• Period: Tangens funksiyasının \( \pi \) dövrü var, yəni \(x\) oxu boyunca hər \( \pi \) vahidində özünü təkrarlayır.
• Asimptom: Tangens funksiyası sinus və kosinusun nisbəti olduğundan, kosinus funksiyası sıfıra bərabər olduqda qeyri-müəyyəndir. Bu, \( \frac{ \pi }{2} \)-nin tək qatlarında baş verir ( \( \pm \frac{ \pi }{2} \), \( \pm \frac{ 3 \pi }{2} \) və s.). Bu nöqtələr şaquli asimptotların meydana gəldiyi yerdir.
• Qiyməylər çoxluğu: Tangens funksiyasının qiymətlər çoxluğu (\( - \infty ; \infty ) \) aralığıdır. Çünki funksiya bütün real dəyərləri qəbul edir.
• Simmetriya: Tangens funksiyası tək funksiyadır, yəni koordinat başlanğıcına nəzərən simmetrikdir.
  Başqa sözlə, \( tg(-x) = -tg(x) \)
• Artan funksiya: Tangens funksiyası öz dövrlərinin hər birində daim artır.

2. Kotangens funksiyası ctg(x):
Kotangent funksiyası kosinus funksiyasının sinus funksiyasına nisbəti kimi müəyyən edilir.
\( ctg(x) = \frac{cos(x)}{sin(x)} \)

Kotangens qrafikinin əsas xüsusiyyətləri:

• Period: Kotangens funksiyasının \( \pi \) dövrü var, bu o deməkdir ki, tangens funksiyası kimi \(x\) oxu boyunca hər \( \pi \) vahidi təkrarlanır.
• Asimptom: Kotangens funksiyası kosinus və sinusun nisbəti olduğundan, sinus funksiyası sıfıra bərabər olduqda qeyri-müəyyəndir. Bu, \( \pi \)-nin tam qatlarında baş verir ( \(0\), \( \pm \pi \), \( \pm 2 \pi \) və s.). Bu nöqtələr şaquli asimptotların meydana gəldiyi yerlərdir.
• Qiymətlər çoxluğu: Kotangens funksiyasının qiymətlər çoxluğu ( \( - \infty ; \infty \) ) aralığıdır. Çünki funksiya bütün real dəyərləri qəbul edir.
• Simmetriya: Kotangens funksiyası tək funksiyadır, yəni koordinat başlanğıcına görə simmetrikdir.
  Başqa sözlə, \( ctg(-x) = -ctg(x) \)
• Azalan funksiya: Kotangens funksiyası öz dövrlərinin hər biri üçün həmişə azalır.

Tərs triqonometrik funksiyalar ☰

Tərs triqonometrik funksiyaları və ya ark-triqonometrik funksiyalar kimi də tanınan tərs triqonometrik funksiyalar əsas triqonometrik funksiyaların tərs funksiyalarıdır. Bu funksiyalar triqonometrik dəyəri bildiyiniz zaman bucağı tapmağa imkan verir. Altı əsas tərs triqonometrik funksiya var:

1. arksinus
\( sin^{-1} (x) \) və ya \( arcsin(x) \): Sinus funksiyasının tərsi.
Təyin oblastı: \( [-1 , 1 ] \)
Qiymətlər çoxluğu: \( [- \frac{ \pi }{2}, \frac{ \pi }{2} ] \)

2. arkkosinus
\( cos^{-1} (x) \) və ya \( arccos(x) \): Kosinus funksiyasının tərsi.
Təyin oblastı: \( [-1 , 1 ] \)
Qiymətlər çoxluğu: \( [ 0 , \pi ] \)

3. arktangens
\( tan^{-1} (x) \) və ya \( arctg(x) \): Tangens funksiyasının tərsi.
Təyin oblastı: \( (- \infty , \infty ) \)
Qiymətlər çoxluğu: \( ( - \frac{ \pi }{2}, \frac{ \pi }{2} ) \)

4. arkkosekant
\( cosec^{-1} (x) \) və ya \( arccosec(x) \): Kosekant funksiyasının tərsi.
Təyin oblastı: \( (-\infty, -1] \cup [1, \infty) \)
Qiymətlər çoxluğu: \( \left[-\frac{\pi}{2}, 0\right) \cup \left(0, \frac{\pi}{2}\right]\)

5. arksekant
\( sec^{-1} (x) \) və ya arcsec(x) \): Sekant funksiyasının tərsi.
Təyin oblastı: \( \left(-\infty, -1\right] \cup \left[1, \infty\right) \)
Qiymətlər çoxluğu: \( \left[0, \frac{\pi}{2}\right) \cup \left(\frac{\pi}{2}, \pi\right] \)

6. arkkotangens
\( ctg^{-1} (x) \) və ya \( arcctg(x) \): Kotangens funksiyasının tərsi.
Təyin oblastı: ( \(- \infty , \infty \) )
Qiymətlər çoxluğu: ( \( 0 , \pi \) )


Tərs triqonometrik funksiyaların bəzi xassələri:

⠐ İşarələmə: Əks triqonometrik funksiyalar çox vaxt " \( ^{-1} \) " və ya "\(arc\)" prefiksi ilə işarələnir.
Məsələn, \( sin^{-1} (x) \) və ya \( arcsin (x) \) tərs sinus funksiyasını təmsil edir. Diqqət edin ki, \( sin^{-1} (x) \) funksiyası \( \frac{1}{sin(x)} \) ilə EYNİ DEYİL.

⠐ Kompozisiya:
Girişin müəyyən qiymətlər çoxluğunda olması şərti ilə triqonometrik funksiya və onun tərs funksiyasının kompozisiyası eynilik funksiyası ilə nəticələnir:

\( sin( arcsin(x) ) = x \), əgər \(x\) \( arcsin( [-1,1] ) \) qiymətlər çoxluğunda olarsa.

\( arcsin ( sin(x) ) = x \), əgər \(x\) \( arcsin( [ -\frac{ \pi }{2} , \frac{ \pi }{2} ] ) \) qiymətlər çoxluğunda olarsa.

Oxşar əlaqələr digər tərs triqonometrik funksiyalar üçün də keçərlidir.

⠐ Diferensiallaşma:
Tərs triqonometrik funksiyalar, orijinal triqonometrik funksiyaların şaquli tangenslərə malik olduğu nöqtələr istisna olmaqla, öz təyin oblastlarında diferensiallaşa bilər.
Məsələn, tərs sinus və kosinus funksiyaları \( x = -1 \) və \( x = 1 \)-də diferensiallaşmır.

⠐ Simmetriya:
Bəzi tərs triqonometrik funksiyalar simmetriya nümayiş etdirir.
Məsələn:
\( arctan(-x) = -arctan(x) \) : Tərs tangens funksiyası tək funksiyadır.

\( arccot(-x) = \pi - arcctg(x) \) : Tərs kotangens funksiyası xüsusi simmetriya növü nümayiş etdirir.

⠐ Törəmələri:
Tərs triqonometrik funksiyaların törəmələri hesablamada, xüsusən də triqonometrik funksiyaları əhatə edən inteqrasiya məsələlərini həll edərkən vacibdir. Üç əsas tərs triqonometrik funksiyanın törəmələri bunlardır:

\( \frac{d (\arcsin(x))}{dx} = \frac{1}{\sqrt{1 - x^2}} \)

\( \frac{d (\arccos(x))}{dx} = -\frac{1}{\sqrt{1 - x^2}} \)

\( \frac{d (\arctan(x))}{dx} = \frac{1}{1 + x^2} \)