Funksiyaların təyin oblastı və qiymətlər çoxluğu ☰

Funksiya hər bir giriş üçün unikal çıxış təyin edən riyazi obyektdir. Bütün mümkün girişlərin çoxluğuna funksiyanın təyin oblastı, bütün mümkün çıxışların çoxluğuna isə funksiyanın qiymətlər çoxluğu deyilir. Başqa sözlə desək, X çoxluğunun hər bir x elementinə Y çoxluğunun müəyyən bir y elementini qarşı qoyan qaydaya X çoxluğunda təyin olunmuş funksiya deyilir.
Burada x sərbəst dəyişən və ya arqument, y isə asılı dəyişən və ya funksiya adlanır. Funksiyanı adətən f ilə, arqumentin verilmiş qiymətinə uyğun qiymətini isə \( f(x) \) ilə işarə edirlər: \( y=f(x) \)
Arqumentin ala bildiyi qiymətlər çoxluğuna funksiyanın təyin oblastı, arqumentin bu qiymətlərinə uyğun asılı dəyişənin aldığı qiymətlərə isə funksiyanın qiymətlər çoxluğu deyilir. f funksiyasının təyin oblastı adətən \( D(f) \) ilə, qiymətlər çoxluğu isə \( E(f) \) ilə işarə edilir.
Funksiya müxtəlif üsullarla verilə bilər: cədvəllə, uyğun qiymətlər cütləri ilə, asılılıq xəritəsi ilə, qrafiklə, düsturla və s.
Nümunəyə baxaq, \( f(x) = x^2 \) funksiyasını nəzərdən keçirək, burada \(x\) həqiqi ədəddir. \(f\)-in təyin oblastı bütün həqiqi ədədlərin çoxluğudur, çünki istənilən həqiqi ədədi \(f\)-ə daxil etmək olar. Bununla belə, \(f\)-in qiymətlər çoxluğu yalnız qeyri-mənfi real ədədlər toplusudur, çünki \( f(x) \), yəni \( x^2 \) həmişə qeyri-mənfidir.

Funksiyanın təyin oblastını və qiymətlər çoxluğunu taparkən bir neçə şeyi yadda saxlamaq lazımdır:

• Funksiyanın təyin oblastı bütün mümkün girişlərin çoxluğudur. Bu o deməkdir ki, funksiyanın qeyri-müəyyən olmasına səbəb olan hər hansı dəyər (məsələn, sıfıra bölmək və ya mənfi ədədin kvadrat kökünü almaq) təyin oblastında ola bilməz.
• Funksiyanın qiymətlər çoxluğu bütün mümkün çıxışların məcmusudur. Bu o deməkdir ki, funksiya yalnız qiymətlər çoxluğunda olan dəyərləri yarada bilər.
• Fərqli funksiyaların eyni təyin oblastı və/və ya qiymətlər çoxluğuna malik olması mümkündür.
  Məsələn, \( f(x) = x^2 \) və \( g(x)=|x| \) funksiyaları hər ikisi bütün real ədədlərin təyin oblastına və müsbət ədədlərin qiymətlər çoxluğuna malikdirlər.

Funksiyanın təyin oblastının və qiymətlər çoxluğunun necə tapılacağını daha yaxşı başa düşmək üçün bəzi nümunələrə baxaq.

Nümunə 1: \( f(x) = \frac{1}{x} \) funksiyanın təyin oblastı və qiymətlər çoxluğunu müəyyən edin.
\( f(x) \) funksiyası bütün \( x \neq 0 \) üçün müəyyən edilmişdir, çünki sıfıra bölmə qeyri-müəyyəndir. Deməli, \(f\) funksiyasının təyin oblastı sıfırdan başqa bütün həqiqi ədədlərin çoxluğudur, yəni \( (-\infty ; 0) \cup (0 ; \infty ) \).
Göründüyü kimi \( f(x) \) funksiyası sıfırdan başqa istənilən həqiqi ədəd ola bilər. Bu o deməkdir ki, \( f \) funksiyasının qiymətlər çoxluğu da \( (-\infty ; 0 ) \cup ( 0 ; \infty ) \) aralığıdır.

Nümunə 2: \( f(x) = \sqrt{4-x^2} \) funksiyanın təyin oblastı və qiymətlər çoxluğunu müəyyən edin.
\( f(x) \) funksiyası yalnız \( 4 - x^2 \ge 0 \) olan \(x\) qiymətləri üçün müəyyən edilir. Bu bərabərsizliyi həll etməklə \( -2 \le x \le 2 \) alırıq. Buna görə də \(f\)-in təyin oblastı qapalı interval \( [ -2 ; 2 ] \)-dir. Təyin oblastından götürülmüş istənilən \(x\) üçün \( 0 \le 4 -x^2 \le 4 \) olur. Bu o deməkdir ki, \(f\)-in qiymətlər çoxluğu qapalı interval \( [ 0 ; 2 ] \)-dir.

Nümunə 3: \( f(x) = sin(x) \) funksiyanın təyin oblastı və qiymətlər çoxluğunu müəyyən edin.
\( f(x) \) funksiyası bütün həqiqi ədədlər üçün müəyyən edilmişdir, ona görə də \( f \)-in təyin oblastı \( (-\infty , \infty) \).
\( sin(x) \), -1 və 1 daxil olmaqla istənilən qiymət ala bilər. Buna görə də \(f\)-in qiymətlər çoxluğu qapalı intervaldır \( [-1,1] \).

Xülasə, funksiyanın təyin oblastı bütün mümkün girişlərin, qiymətlər çoxluğu isə bütün mümkün çıxışların çoxluğudur. Təyin oblastı və qiymətlər çoxluğu funksiyanın özünü və ya qrafikini təhlil etməklə müəyyən edilə bilər.

Funksiyaların xassələri ☰

Funksiyaların təhlili və müqayisəsi üçün istifadə oluna bilən müxtəlif xüsusiyyətlər var. Bu bölmədə funksiyaların ən vacib xüsusiyyətlərindən bəzilərini müzakirə edəcəyik.
Funksiyanın qrafikinin absis oxu ilə kəsişmə nöqtələrində \( f(x) = 0 \) olur. Arqumentin funksiyanı sıfıra çevirən qiymətlərinə funksiyanın sıfırları deyilir.

Cüt və tək funksiyalar:
Təyin oblastı \( x = 0 \) nöqtəsinə nəzərən simmetrik olan funksiyalarda təyin oblastından götürülmüş ixtiyari \(x\) üçün \( f(-x) = f(x) \) olarsa \( f(x) \)-ə cüt funksiya deyilir. Başqa sözlə desək, cüt funksiyalarda funksiyanın qrafiki \(y\) oxuna nəzərən simmetrikdir. Cüt funksiyaya misal olaraq \( f(x) = x^2 \) göstərilə bilər.
Təyin oblastı \( x = 0 \) nöqtəsinə nəzərən simmetrik olan funksiyalarda təyin oblastından götürülmüş ixtiyari \(x\) üçün \( f(-x) = -f(x) \) olarsa \( f(x) \)-ə tək funksiya deyilir. Başqa sözlə desək, tək funksiyalarda funksiyanın qrafiki koordinat başlanğıcına nəzərən simmetrikdir. Tək funksiyaya misal olaraq \( f(x) = x^3 \) göstərilə bilər.
Not. Funksiyanın təyin oblastı 0 nöqtəsinə nəzərən simmetrik olmazsa və ya \( f(-x) = f(x) \) , \( f(-x) = -f(x) \) şərtlərini ödəməzsə onda belə funksiya nə tək, nə də cüt funksiya adlanır.

Artan və Azalan funksiya: Təyin oblastının müəyyən aralığından götürülmüş \( x_1 < x_2 \) şərtini ödəyən ixtiyari \( x_1 , x_2 \) üçün \( f(x_1 ) < f(x_2 ) \) olarsa, yəni arqumentin böyük qiymətinə funksiyanın böyük qiyməti uyğundursa, bu aralıqda \( f(x) \)-ə artan, \( f(x_1 )> f(x_2 ) \) olarsa, yəni arqumentin böyük qiymətinə funksiyanın kiçik qiyməti uğun gələrsə, \( f(x) \)-ə bu aralıqda azalan funksiya deyilir.
Bucaq əmsalının işarəsinə görə xətti funksiyanın artan və ya azalan olduğunu müəyyən etmək olar.
Bucaq əmsalı müsbət olan xətti funksiya artandır.
Bucaq əmsalı mənfi olan xətti funksiya azalandır.
Verilmiş aralıqda artan və ya azalan funksiyalara həmin aralıqda monoton funksiyalar deyilir.
Qrafik üzərində artmanın azalma ilə və ya azalmanın artma ilə əvəz olunduğu nöqtələr uyğun olaraq, funksiyanın maksimum və minimumunu göstərir.
\( x_0 \) nöqtəsinin daxil olduğu ixtiyari intervala bu nöqtənin ətrafı deyilir.
\( x_0 \)-ın müəyyən ətrafında \( x_0 \)-dan fərqli bütün \( x \)-lər üçün \( f(x) > f(x_0 ) \) olarsa, \( x_0 \)-a \( f(x) \)-in minimum nöqtəsi, \( f(x_0 ) \)-a isə minimum qiyməti deyilir.
\( x_0 \)-ın müəyyən ətrafında \( x_0 \)-dan fərqli bütün \(x\)-lər üçün \( f(x) < f(x_0 ) \) olarsa, \( x_0 \)-a \( f(x)\) -in maksimum nöqtəsi, \( f(x_0 ) \)-a isə maksimum qiyməti deyilir. Maksimum və minimum nöqtələri \(x_{max} \) , \(x_{min} \) kimi işarə edilir və ekstremum nöqtələri, funksiyanın bu nöqtələrdəki qiymətləri isə ekstremumları adlanır.
Qrafiki verilmiş funksiya \( x = c \) nöqtəsində minimuma, \( x = d \) nöqtəsində isə maksimuma malik olduqda \( x_{min} = c \) , \( f_{min} = f(c) \), \( x_{max} = d \) , \( f_{max} = f(d) \) şəklində yazılır.
Bütün təyin oblastında funksiyanın qiymətləri içərisində ən böyüyü ƏBQ , ən kiçiyi isə ƏKQ ilə işarə edilir (əgər varsa). Funksiya kəsilməzdirsə (verilmiş aralıqda qrafiki bütöv xətdirsə),ƏKQ ilə ƏBQ arasındakı bütün qiymətləri alır.

Dövri funksiya:
Tutaq ki, elə \( T \neq 0 \) ədədi var ki, funksiyanın təyin oblastından götürülmüş istənilən \(x\) üçün \(x \pm T \)-də təyin oblastına daxildir və \(f(x-T) = f(x) = f(x+T) \) ödənir. Onda \(f(x) \) funksiyasına dövrü \(T\) olan dövri funksiya deyilir. Funksiyanın ən kiçik müsbət dövrünə onun əsas dövrü deyilir.

• "T" ədədi "f" funksiyasının dövrüdürsə "(-T)" ədədi də "f" funksiyasının dövrü olur.
• \( T_1 \) və \(T_2 \) ədədləri f funksiyasının dövrüdürsə \( T_1 + T_2 \) və \( T_1 - T_2 \) ədədləri də f funksiyasının dövrü olur.
• T ədədi f funksiyasının dövrüdürsə, n istənilən tam ədəd olduqda "nT" ədədi də f funksiyasının dövrüdür. \( y = f(x) \) funksiyası dövridirsə, onun dövrlərinin sayı sonsuzdur.
  Buradan da dediklərimizi ümumiləşdirsək, $$ f(x) = f(x+T) = f(x+2T) =... = f(x+3T) = ⋯ = f(x+nT) = ⋯ $$ alınacaq.
• \( y = f(x) \) dövri funksiyadırsa, onun təyin oblastı koordinat başlanğıcına nəzərən simmetrikdir və sonsuz çoxluqdur.

Dövri funksiyaya nümunə olaraq \( f(x) = sin(x) \) funksiyasını göstərmək olar.

Funksiyaların təsnifatı ☰

Bu bölmədə bəzi əsas funksiyalar haqqında bir sıra məlumatlarla tanış olacağıq.

Sabit funksiya:
\(F(x) = c.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = \{c\}.\)


Eynilik funksiyası:
\(F(x) = x.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = (-\infty, +\infty).\)
Sıfırı: \( x=0 \).
Artan funksiyadır.
Ekstremumu yoxdur.


Modul funksiyası:
\(F(x) = |x|.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = [0, +\infty).\)
Sıfırı: \(x = 0.\)
\((- \infty, 0] \downarrow \text{, } [0, +\infty) \uparrow.\)
Minimum nöqtəsi: \((0, 0).\)


Rasional funksiya:
\(F(x) = \frac{1}{x}.\)
\(D(f) = (-\infty, 0) \cup (0, +\infty).\)
\(E(f) = (-\infty, 0) \cup (0, +\infty).\)
\((- \infty, 0) \downarrow \text{, } (0, +\infty) \downarrow.\)
Sıfırı yoxdur.
Ekstremumu yoxdur.


Kvadrat funksiyası:
\(F(x) = x^2.\)
\( D(f) = (-\infty, +\infty). \)
\( E(f) = [0, +\infty). \)
\((- \infty, 0] \downarrow \text{, } [0, +\infty) \uparrow.\)
Sıfırı: \(x = 0.\)
Minimum nöqtəsi: \((0, 0).\)


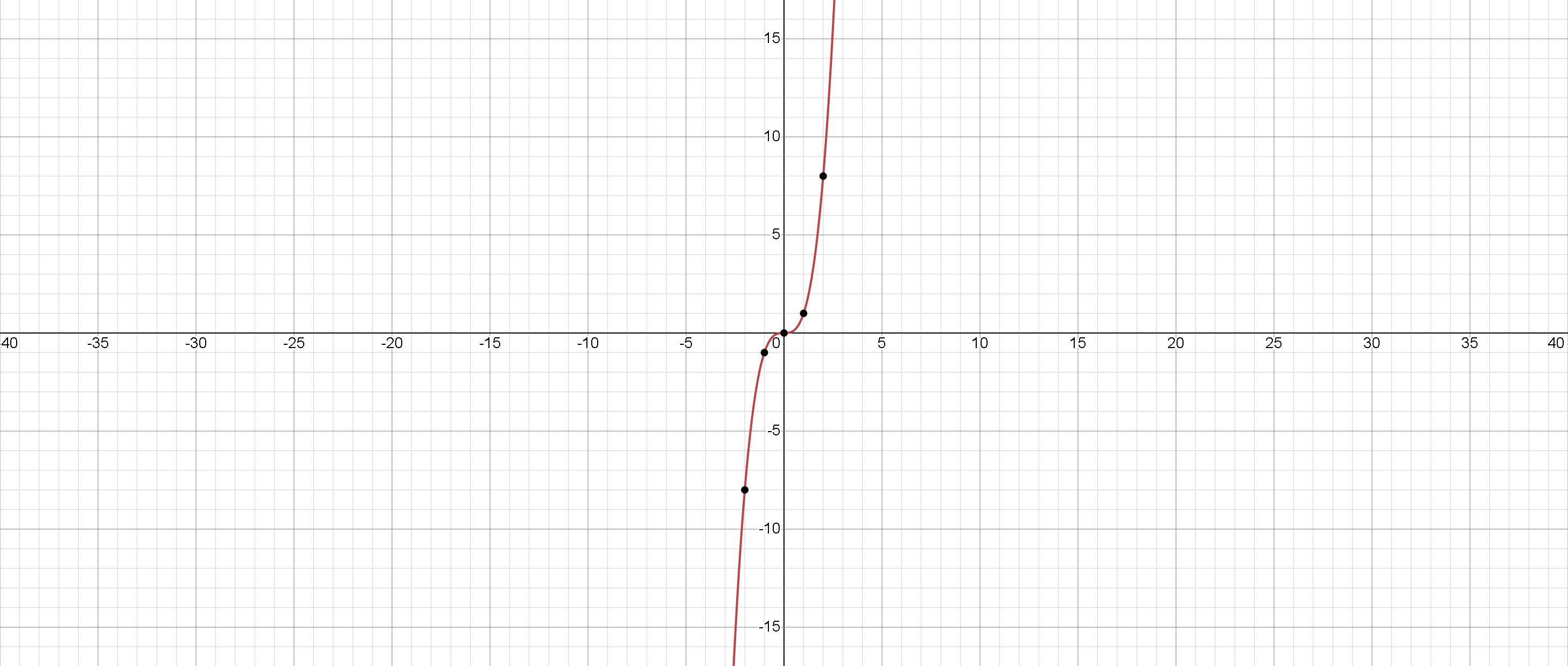
Kub funksiyası:
\(F(x) = x^3.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = (-\infty, +\infty).\)
Sıfırı: \(x = 0.\)
Artan funksiyadır.
Ekstremumu yoxdur.


Kvadrat kök funksiyası:
\(F(x) = \sqrt{x}.\)
\(D(f) = [0; +\infty).\)
\(E(f) = [0; +\infty).\)
Sıfırı: \(x = 0.\)
\( [0; +\infty) \uparrow \).
Ekstremumu yoxdur.


Triqonometrik funksiyalar:
Triqonometrik funksiya düzbucaqlı üçbucağın tərəflərinin nisbətlərini ehtiva edən funksiyadır. Triqonometrik funksiyalara misal olaraq \( sin(x) \), \( cos(x) \) və \( tan(x) \) funksiyalarını göstərmək olar.
Triqonometrik funksiyaların qrafikləri dövri xarakter daşıyır və müəyyən bir intervaldan sonra təkrarlanır.

Hissə-hissə verilmiş funksiyalar:
Təyin oblastının müxtəlif aralıqlarında müxtəlif düsturlarla verilən funksiyalara hissə-hissə verilmiş funksiyalar deyilir.

Məsələn:
\( f(x) = \begin{cases} 2x + 1, & x < 0 \text{ olduqda} \\ 3x, & x \geq 0 \text{ olduqda} \end{cases} \)

\( f(x) = \begin{cases} x^2, & x \leq -1 \\ -x, & -1 < x < 1 \\ x, & x \geq 1 \end{cases} \)

Natural üstlü qüvvət funksiyası ☰

\(n\) natural ədəd olduqda \(y= x^n \) şəklində funksiyaya natural üstlü qüvvət funksiyası deyilir.
\( y= x^n \) funksiyasının qrafiki \(n\)-in istənilən cüt qiymətində ordinat oxuna nəzərən simmetrikdir və \(y= x^2 \) parabolasına oxşardır.
\(n\)-in istənilən tək qiymətində \(y= x^n \) funksiyasının qrafiki koordinat başlanğıcına nəzərən simmetrikdir və \(n\)-in 1-dən böyük tək qiymətlərində \(y= x^3 \)-ün qrafiki olan kub parabolaya oxşardır.

\( \mathbf {F(x)= x^{2k}} \) olduqda:
\( D(f) = (-\infty ; +\infty) \).
\( E(f) = [0; +\infty). \)
Sıfırı: \(x=0 \).
\( (-\infty; 0] \downarrow \text{, } [0; +\infty) \uparrow \).
\( x_{\text{min}} = 0, f_{\text{min}} = 0 \).
Ekstremumu yoxdur.

\( \mathbf{ F(x) = x^{2k+1} } \) olduqda:
\( D(f) = (-\infty ; +\infty). \)
\( E(f) = (-\infty ; +\infty). \)
Sıfırı: \( x=0 \).
\( (-\infty ; +\infty) \uparrow \)
Ekstremumu yoxdur.

\( n > 1 \),\( n \in N \) olduqda \( x^n \) funksiyasının qrafiki \( \mathbf{n} \) tərtibli parabola adlanır.
\( n > m \) olduqda \( (0; 1) \) aralığında \(x^n \) funksiyasının qrafiki \(x^m \) funksiyasının qrafikindən aşağıda, \( (1; +\infty ) \) aralığında isə yuxarıda yerləşir.
Ümumiyyətlə, \( y= x^n \) funksiyalar ailəsi \(n\) dəyərindən asılı olaraq müxtəlif davranışlar nümayiş etdirir.
Bu funksiyaların qrafiki xətlər, əyrilər və fasiləsiz sıçrayışlar da daxil olmaqla müxtəlif formalara malik ola bilər. Bu funksiyaların öyrənilməsi riyaziyyat və elmdə vacibdir, çünki onlar bir çox təbiət hadisələrində və mühəndislik tətbiqlərində görünürlər.

Bəzi mühüm xassələri:

• \(y = x^n \) funksiyasının törəməsi \( y' = n \cdot x^{n-1} \) ilə verilir. Bu o deməkdir ki, hər hansı bir nöqtədə funksiyaya toxunan xəttin mailliyi \(n\)-in qiyməti ilə mütənasibdir.
• \( y = x^n \) funksiyasının inteqralı \( \int x^n \, dx = \frac{x^{n+1}}{n+1} + C \) ilə verilir, burada \(C\) inteqral sabitidir. Bu düstur \(n= -1 \) olduğu hallar istisna olmaqla, \(n\)-nin bütün qiymətlərinə aiddir, bu halda inteqral \( \ln |x| + C \) ilə verilir.

Funksiyalar üzərində əməllər ☰

Riyaziyyatda funksiyalar üzərində əməllər funksiyalar üzərində yerinə yetirilə bilən riyazi əməliyyatlara aiddir. Bu əməliyyatlar yeni funksiyalar yaratmaq üçün funksiyaları manipulyasiya etmək və ya birləşdirmək üçün istifadə edilə bilər. Funksiyalar üzərində ən çox yayılmış əməliyyatlara toplama, çıxma, vurma, bölmə, kompozisiya və tərs funksiya daxildir.

Funksiyaların toplanması və çıxılması:
Yeni funksiya yaratmaq üçün funksiyalar toplana və ya çıxıla bilər. İki \( f(x) \) və \( g(x) \) funksiyasını nəzərə alaraq, hər iki funksiyanın cəmi və ya fərqi \( (f \pm g ) (x) \) ilə işarələnir və aşağıdakı kimi müəyyən edilir:
\( (f+g) (x) = f(x)+ g(x) \)
\( (f-g) (x) = f(x)- g(x) \)
İki cüt funksiyanın cəmi cüt, iki tək funksiyanın cəmi tək funksiyadır.

Nümunə: \( f(x) = x+1 \) və \( g(x) = 2x-3 \) funksiyalarını toplayaq və çıxaq.
\( \small (f+g) (x) = f(x) + g(x) = (x+1) + (2x-3) = 3x-2 \)
\( \small (f-g) (x) = f(x) - g(x) = (x+1) - (2x-3) = -x+4 \)

Funksiyaların vurulması və bölünməsi:
Yeni funksiyalar yaratmaq üçün funksiyalar vurula və ya bölünə bilər. İki \( f(x) \) və \( g(x) \) funksiyasını nəzərə alaraq, iki funksiyanın hasili və ya nisbəti \( (f \cdot g) (x) \) və ya \( (\frac{f}{g}) (x) \) ilə işarələnir və aşağıdakı kimi müəyyən edilir:
\( (f \cdot g)(x) = f(x) \cdot g(x) \)
\( ( \frac{f}{g} )(x) = \frac{f(x)}{g(x)}, \quad g(x) \neq 0 \)

İki cüt funksiyanın və iki tək funksiyanın hasili (nisbəti) cüt funksiya, cüt funksiya ilə tək funksiyanın hasili (nisbəti) tək funksiyadır.

Nümunə: \( f(x) = x+1 \) və \( g(x) = 2x-3 \) funksiyalarını vuraq və bölək.
\( (f \cdot g)(x) = (x+1)(2x-3) = 2x^2 - x - 3 \)
\( (\frac{f}{g})(x) = \frac{x+1}{2x-3} \)

Funksiyaların kompozisiyası (mürəkkəb funksiya):
Funksiyaların kompozisiyası yeni funksiya yaratmaq üçün iki və ya daha çox funksiyanın birləşdirilməsi əməliyyatıdır. İki \( f(x) \) və \( g(x) \) funksiyasını nəzərə alaraq, hər iki funksiyanın tərkibi \( (f \circ g)(x) = f(g(x)) \) ilə işarələnir və belə müəyyən edilir: \( (f \circ g)(x) = f(g(x)) \).

Nümunə: \( f(x) = x^2 \) və \( g(x) = x+1 \) funksiyaların kompozisiyası.
\( (f \circ g) (x) = f(g (x) ) = f(x+1) = (x+1)^2 \)
Diqqət yetirin ki, kompozisiyada ardıcıllıq vacibdir.
Yəni, \( (f \circ g) (x) \) ilə \( (g \circ f) (x) \) eyni deyil.

Tərs funksiya:
Funksiyanın tərsi, orijinal funksiyanı “geri götürən” yeni funksiyadır. \( f(x) \) funksiyası verilmişdirsə, funksiyanın tərsi \( f^{-1} (x) \) ilə işarələnir və belə təyin olunur:
\( f^{-1} (f(x)) = x \)

Bir funksiyanın tərsinin mövcud olması üçün funksiya “bir-bir” olmalıdır. Təyin oblastındaki hər bir element qiymətlər çoxluğundakı unikal elementə uyğunlaşırsa, funksiya “bir-birdir”. Tərs funksiya funksiyanın \(y=x \) xətti boyunca əks olunmasıdır.
Nümunə: \( f(x) = 2x+1 \) funksiyasının tərsi \( f^{-1} (x) = \frac{x-1}{2} \)

Funksiyalar üzərində əməllərin bəzi xassələri:

• Assosiativlik: \( (f+g)+h = f+(g+h) \)
• Kommutativlik: \( f+g=g+f \)
• Paylanma: \( f \cdot (g+h) = f \cdot g + f \cdot h \)