Domain and Range of a functions ☰

A function is a mathematical object that assigns a unique output to every input. The set of all possible inputs is called the domain of the function, and the set of all possible outputs is called the range of the function. In other words, the domain is the set of values that can be plugged into the function, and the range is the set of values that the function can produce.
Formally, a function \(f\) is a mapping from a set \(A\) (the domain) to a set \(B\) (the range), where for each \( a \in A\) , there is a unique \( b \in B \) such that \(f(a)=b \). We write \(f\): \( A \rightarrow B \) to denote that \(f\) is a function from \(A\) to \(B\).
For example, consider the function \(f(x)=x^2\), where \(x\) is a real number. The domain of \(f\) is the set of all real numbers, because any real number can be plugged into \(f\). However, the range of \(f\) is only the set of non-negative real numbers, because \(f(x)\) is always non-negative.
When finding the domain and range of a function, there are a few things to keep in mind:

• The domain of a function is the set of all possible inputs. This means that any value that causes the function to be undefined (such as dividing by zero or taking the square root of a negative number) cannot be in the domain.
• The range of a function is the set of all possible outputs. This means that the function can only produce values that are in the range.
• It is possible for different functions to have the same domain or range. For example, the functions \(f(x)=x^2 \) and \(g(x)=|x| \) both have the domain of all real numbers, but their ranges are different.
• The domain and range of a function can be determined by analyzing the graph of the function. The domain is the set of all possible x-values that appear on the graph, and the range is the set of all possible y-values that appear on the graph.

Let's look at some examples to better understand how to find the domain and range of a function.

Example 1: Find the domain and range of the function \( f(x) = \frac{1}{x} \)
The function \(f(x) \) is defined for all \( x \neq 0 \) because division by zero is undefined. Therefore, the domain of \(f\) is the set of all real numbers except zero, or \( (-\infty ; 0) \cup (0 ; \infty ) \).
To find the range of \(f\), we note that \(f(x) \) can be any real number except zero. This means that the range of \(f\) is also \( (-\infty ; 0 ) \cup ( 0 ; \infty ) \).

Example 2: Find the domain and range of the function \( f(x) = \sqrt{4-x^2} \).
The function \(f(x)\) is defined only for values of \(x\) such that \( 4 - x^2 \ge 0 \). Solving this inequality, we get \( -2 \le x \le 2 \).
Therefore, the domain of \(f\) is the closed interval \([-2,2]\). To find the range of \(f\), we note that \(f(x)\) can be any non-negative real number less than or equal to 2. This means that the range of \(f\) is the closed interval \([0,2]\).

Example 3: Find the domain and range of the function \(f(x)=sin(x) \).
The function \(f(x) \) is defined for all real numbers, so the domain of \(f\) is \( (-\infty , \infty) \).
To find the range of \(f\), we note that \(sin(x)\) can take on any value between -1 and 1, inclusive. Therefore, the range of \(f\) is the closed interval \([-1,1] \).

In summary, the domain of a function is the set of all possible inputs, and the range is the set of all possible outputs. The domain and range can be determined by analyzing the function itself or its graph.

Properties of functions ☰

Functions have various properties that can be used to analyze and compare them. In this explanation, we will discuss some of the most important properties of functions.

Even and Odd Functions:
A function \(f\) is said to be even if \(f(-x)=f(x) \) for all \(x\) in the domain of \(f\). In other words, the function is symmetric with respect to the \(y\)-axis. An example of an even function is \(f(x)=x^2 \).
A function \(f\) is said to be odd if \(f(-x)=-f(x) \) for all \(x\) in the domain of \(f\). In other words, the function is symmetric with respect to the origin. An example of an odd function is \(f(x)=x^3 \).

Increasing and Decreasing Functions:
A function \(f\) is said to be increasing on an interval if \( f(x_1 ) < f(x_2 ) \) whenever \(x_1 < x_2\) and \(x_1, x_2 \) are in the domain of \(f\). In other words, the function is going up as \(x\) increases. An example of an increasing function is \(f(x)=x \).
A function \(f\) is said to be decreasing on an interval if \( f(x_1 ) > f(x_2 ) \) whenever \(x_1 < x_2\) and \(x_1, x_2 \) are in the domain of \(f\). In other words, the function is going down as \(x\) increases. An example of a decreasing function is \(f(x)=-x \).

Periodic Functions:
A function \(f\) is said to be periodic if there exists a positive number \(p\) such that \(f(x+p)=f(x)\) for all \(x\) in the domain of \(f\). In other words, the function repeats itself after a fixed interval. An example of a periodic function is \(f(x)=sin(x)\).

Injective and Surjective Functions:
A function \(f\) is said to be injective (or one-to-one) if for every \(y\) in the range of \(f\), there is exactly one \(x\) in the domain of \(f\) such that \(f(x)=y\). In other words, no two distinct inputs give the same output. An example of an injective function is \( f(x)=x+1 \).
A function \(f\) is said to be surjective (or onto) if for every \(y\) in the range of \(f\), there is at least one \(x\) in the domain of \(f\) such that \(f(x)=y\). In other words, every output in the range is achieved by some input. An example of a surjective function is \( f(x)=x^2 \).

Bijective Functions:
A function \(f\) is said to be bijective if it is both injective and surjective. In other words, every output in the range is achieved by exactly one input. An example of a bijective function is \( f(x)= \sqrt{x} \).

In summary, the properties of functions can be used to describe various aspects of the function, such as its symmetry, direction, repetition, and correspondence between inputs and outputs. Understanding these properties can help in analyzing and comparing functions in different contexts.

Classification of functions ☰

Functions can be classified based on their properties and behavior. In this explanation, we will discuss the most common classifications of functions.

Constant function:
\(F(x) = c.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = \{c\}.\)


Linear function:
\(F(x) = x.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = (-\infty, +\infty).\)
Zeros: \( x=0 \).
Increased function.
No extremum.


Absolute value function:
\(F(x) = |x|.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = [0, +\infty).\)
Zeros: \(x = 0.\)
\((- \infty, 0] \downarrow \text{, } [0, +\infty) \uparrow.\)
Minimum point: \((0, 0).\)


Rational function:
\(F(x) = \frac{1}{x}.\)
\(D(f) = (-\infty, 0) \cup (0, +\infty).\)
\(E(f) = (-\infty, 0) \cup (0, +\infty).\)
\((- \infty, 0) \downarrow \text{, } (0, +\infty) \downarrow.\)
No zeros.
NO extremum.


Quadratic function:
\(F(x) = x^2.\)
\( D(f) = (-\infty, +\infty). \)
\( E(f) = [0, +\infty). \)
\((- \infty, 0] \downarrow \text{, } [0, +\infty) \uparrow.\)
Zeros: \(x = 0.\)
Minimum point: \((0, 0).\)


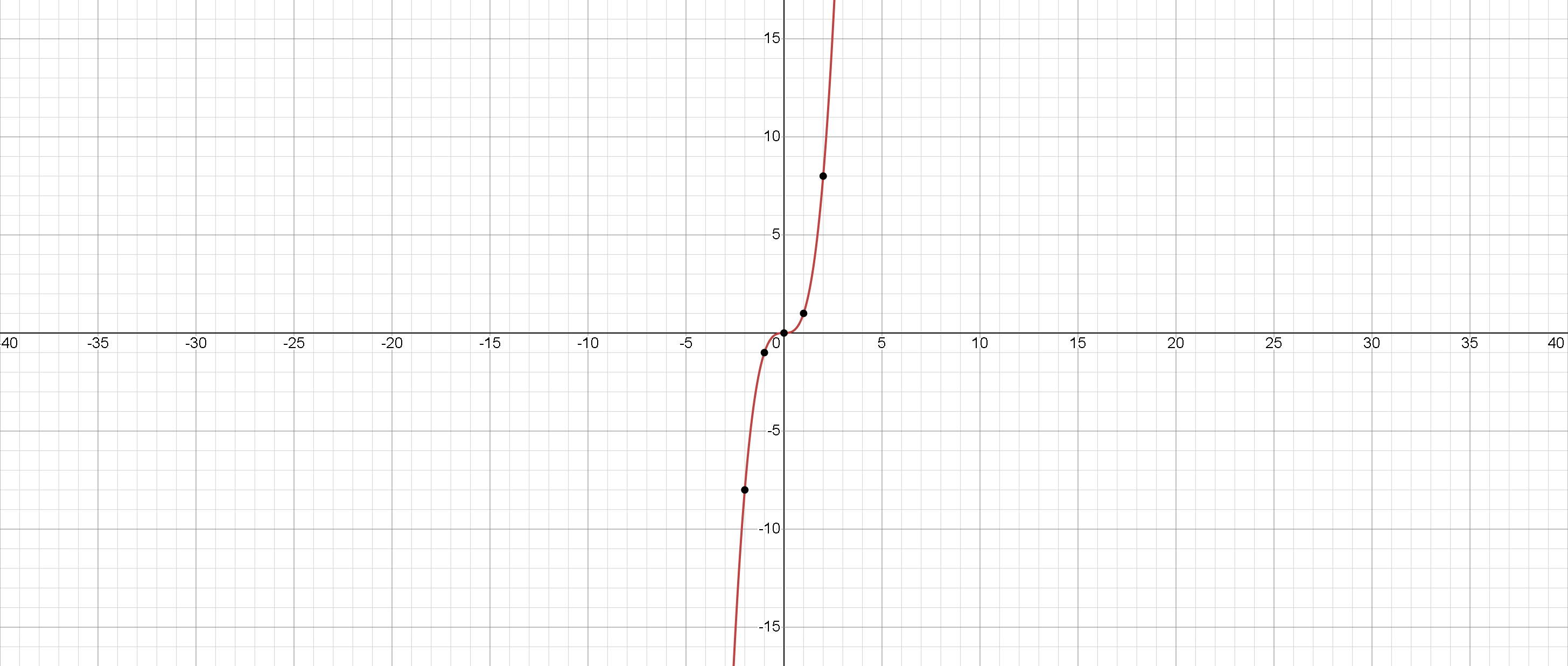
Cubic function:
\(F(x) = x^3.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = (-\infty, +\infty).\)
Zeros: \(x = 0.\)
Increased function.
No extremum.


Square Root function:
\(F(x) = \sqrt{x}.\)
\(D(f) = [0; +\infty).\)
\(E(f) = [0; +\infty).\)
Zeros: \(x = 0.\)
\( [0; +\infty) \uparrow \).
No extremum.


Trigonometric Functions:
A trigonometric function is a function that involves the ratios of the sides of a right triangle. Examples of trigonometric functions include \( sin(x) \), \( cos(x) \), and \( tan(x) \). The graphs of trigonometric functions are periodic and repeat themselves after a fixed interval.

Piecewise Functions:
A piecewise function is a function that is defined by different equations on different parts of its domain.

Examples of piecewise functions include:
\( f(x) = \begin{cases} 2x + 1 & \text{if } x < 0 \\ 3x & \text{if } x \geq 0 \end{cases} \)

\( f(x) = \begin{cases} x^2 & \text{if } x \leq -1 \\ -x & \text{if } -1 < x < 1 \\ x & \text{if } x \geq 1 \end{cases} \)

Power functions or Monomials ☰

These functions are also known as power functions or monomials.
The value of the exponent \(n\) determines the shape and behavior of the function. When \(n\) is a positive integer, the function represents a polynomial with a single term, known as a monomial. The degree of the polynomial is equal to the value of \(n\).

\( F(x)= x^{2k} \):
\( D(f) = (-\infty ; +\infty) \).
\( E(f) = [0; +\infty). \)
Zeros: \(x=0 \).
\( (-\infty; 0] \downarrow \text{, } [0; +\infty) \uparrow \).
\( x_{\text{min}} = 0, f_{\text{min}} = 0 \).
No extremum.

\( F(x) = x^{2k+1} \):
\( D(f) = (-\infty ; +\infty). \)
\( E(f) = (-\infty ; +\infty). \)
Zeros: \( x=0 \).
\( (-\infty ; +\infty) \uparrow \)
No extremum.

For example, the function \(y=x^2\) represents a parabola, which is a U-shaped curve that opens upwards. This function has a minimum value at \(x=0\) and increases without bound as \(x\) moves away from zero in either direction.
When \(k\) is a negative integer, the function represents a reciprocal of a monomial. For example, the function \(y = x^{-1} \) represents the reciprocal function, also known as the inverse function. This function has a vertical asymptote at \(x=0\), where the function approaches positive or negative infinity depending on the sign of \(x\). The reciprocal function is symmetric about the line \(y=x\).
When \(2k =n\) or \(2k+1 = n\) is a fraction, the function represents a radical function, where the numerator of the fraction determines the degree of the root and the denominator determines the power of \(x\). For example, the function \( y = x^\frac{1}{2} \) represents the square root function, which has a domain of non-negative real numbers and a range of non-negative real numbers. The square root function is a half-parabola that opens to the right and has a vertical asymptote at \(x=0\).
In general, the \(y=x^n\) functions family of functions exhibit a variety of behaviors depending on the value of \(n\). The graph of these functions can have different shapes, including lines, curves, and discontinuous jumps. The study of these functions is important in mathematics and science, as they appear in many natural phenomena and engineering applications.

Some important properties of these functions include:

• When \(n\) is even, the function \(y=x^n\) is always non-negative for all real values of \(x\). When \(n\) is odd, the function can take on both positive and negative values depending on the sign of \(x\).
• When \(n\) is positive, the function \(y=x^n\) is increasing on the interval \( (0, \infty) \) and decreasing on the interval \( (-\infty, 0) \). When \(n\) is negative, the function has the opposite behavior.
• The derivative of the function \(y=x^n\) is given by \( y'=nx^{n-1} \). This means that the slope of the tangent line to the function at any point is proportional to the value of the exponent \(n\).
• The integral of the function \(y=x^n\) is given by \( \int x^n \, dx = \frac{x^{(n+1)}}{(n+1)} + C \), where \(C\) is a constant of integration. This formula holds for all values of \(n\) except when \(n=-1\), in which case the integral is given by \( ln|x|+C \).

In summary, the \(y=x^n\) functions family of functions is a fundamental topic in mathematics, with many important applications in various fields. The behavior and properties of these functions depend on the value of the exponent \(n\), which determines the shape of the graph and other important features.

Operations on functions ☰

In mathematics, operations on functions refer to mathematical operations that can be performed on functions. These operations can be used to manipulate or combine functions to create new functions. The most common operations on functions include addition, subtraction, multiplication, division, composition, and inverse.

Addition and Subtraction of Functions:
Functions can be added or subtracted to create a new function. Given two functions \(f(x)\) and \(g(x)\), the sum or difference of the two functions is denoted by \( (f \pm g)(x) \) and is defined as:
\( (f+g) (x) = f(x)+ g(x) \)
\( (f-g) (x) = f(x)- g(x) \)
The sum of two even functions is even, and the sum of two odd functions is odd.

For example: \( f(x) = x+1 \) and \( g(x) = 2x-3 \) functions.
\( \small (f+g) (x) = f(x) + g(x) = (x+1) + (2x-3) =\) \( 3x-2 \)
\( \small (f-g) (x) = f(x) - g(x) = (x+1) - (2x-3) =\) \( -x+4 \)

Multiplication and Division of Functions:
Functions can also be multiplied or divided to create new functions. Given two functions \(f(x)\) and \(g(x)\), the product or quotient of the two functions is denoted by \( (f \cdot g) (x) \) or \( (\frac{f}{g}) (x) \) and is defined as:
\( (f \cdot g)(x) = f(x) \cdot g(x) \)
\( ( \frac{f}{g} )(x) = \frac{f(x)}{g(x)}, \quad g(x) \neq 0 \)

The product (ratio) of two even functions and two odd functions is an even function, and the product (ratio) of an even function and an odd function is an odd function.

For example: \( f(x) = x+1 \) and \( g(x) = 2x-3 \) functions.
\( (f \cdot g)(x) = (x+1)(2x-3) = 2x^2 - x - 3 \)
\( (\frac{f}{g})(x) = \frac{x+1}{2x-3} \)

Composition of Functions:
Composition of functions is the operation of combining two or more functions to create a new function. Given two functions \( f(x) \) and \( g(x) \), the composition of the two functions is denoted by \( (f \circ g)(x) \) and is defined as: \( (f \circ g)(x) = f(g(x)) \).

For example: \( f(x) = x^2 \) and \( g(x) = x+1 \) functions.
\( (f \circ g) (x) = f(g (x) ) = f(x+1) = (x+1)^2 \)
Note that the order of composition matters, i.e., \( (f \circ g)(x) \) is not the same as \( (g \circ f)(x) \).

Inverse of a Function:
The inverse of a function is a new function that "undoes" the original function. Given a function \(f(x) \), the inverse of the function is denoted by \(f^{-1} (x) \) and is defined as:
\( f^{-1} (f(x)) = x \)

For the inverse of a function to exist, the function must be one-to-one. A function is one-to-one if each element in the domain maps to a unique element in the range. The inverse function is the reflection of the function across the line \(y=x\).
For example: If \( f(x) = 2x+1 \) , then \( f^{-1} (x) = \frac{x-1}{2} \)
To verify this, we can check that \( f^{-1} (f(x))= \frac{2x+1-1}{2} = x \).

Here are some additional details about operations on functions:

Properties of Operations on Functions:
The operations on functions have some properties that make them useful for solving mathematical problems. These properties include:

• Associativity: The order in which the operations are performed does not affect the result.
  For example, \( (f+g)+h = f+(g+h) \)
• Commutativity: The order of the functions does not affect the result.
  For example, \( f+g=g+f \)
• Distributivity: The operation distributes over another operation.
  For example, \( f \cdot (g+h) = f \cdot g + f \cdot h \)

Domains and Ranges:
When performing operations on functions, it is important to consider the domains and ranges of the functions. The domain of a function is the set of values for which the function is defined, while the range is the set of values that the function can take.
When adding or subtracting functions, the domains and ranges of the functions should be the same. When multiplying or dividing functions, the domain of the resulting function should be the intersection of the domains of the two functions, and the range of the resulting function may be restricted by the range of the denominator.
When composing functions, the range of the inner function should be a subset of the domain of the outer function.

Transformations of Functions:
Operations on functions can also be used to transform functions. For example, adding a constant to a function shifts the function vertically, while multiplying a function by a constant scales the function vertically. Similarly, adding a variable to a function shifts the function horizontally, while multiplying a function by a variable scales the function horizontally.