Квадратичная функция и её график☰

Квадратичная функция - это многочленная функция степени два. Она определяется формулой: \( f(x)=ax^2+bx+c \), где \(a\), \(b\) и \(c\) - константы, и \(a\) не равно нулю.
График квадратичной функции - это парабола, которая представляет собой кривую в форме буквы U. Направление параболы зависит от знака ведущего коэффициента \(a\). Если \(a\) положительное, то парабола открывается вверх, а если \(a\) отрицательное, то парабола открывается вниз.
Вершина параболы определяется формулой: \(\left(-\frac{b}{2a}, \frac{4ac - b^2}{4a}\right)\).

Ось симметрии параболы - это вертикальная линия, проходящая через вершину и задаваемая уравнением \(x=-\frac{b}{2a}\).

\(x\)-пересечения (нули) квадратичной функции определяются квадратным уравнением: \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \).
Если дискриминант \(b^2-4ac\) положителен, у квадратичной функции есть два различных вещественных корня, которые являются \(x\)-координатами \(x\)-пересечений. Если дискриминант равен нулю, у квадратичной функции есть один вещественный корень, который является \(x\)-координатой вершины. Если дискриминант отрицателен, у квадратичной функции нет вещественных корней, но есть два комплексно сопряженных корня.

Квадратичные функции также могут быть записаны в факторизованной форме: \( f(x)=a(x-r_1 )(x-r_2 ) \), где \(r_1\) и \(r_2\) - корни квадратичной функции. Эта форма полезна для нахождения корней функции.
Вершинная форма квадратичной функции: \( f(x)=a(x-h)^2 +k \), где \( (h,k) \) - вершина параболы. Стандартная форма и вершинная форма квадратичной функции связаны следующим образом: \( f(x)=a(x-h)^2 +k=ax^2 -2ahx+ah^2 +k \), что показывает, что \(a\), \( b=-2ah \) и \( c=ah^2 +k\) связаны с вершиной \( (h,k) \).
Квадратичная функция может быть построена путем построения вершины, оси симметрии и \(x\)-пересечений. Для наброска графика мы также можем найти максимальное или минимальное значение функции, область определения, область значений и любые преобразования или сдвиги.

Максимальное или минимальное значение квадратичной функции:
Если \( a > 0 \), парабола открывается вверх, и вершина является минимальной точкой функции. Минимальное значение равно \( f(h)=k \). Если \( a < 0 \), парабола открывается вниз, и вершина является максимальной точкой функции. Максимальное значение равно \(f(h)=k\).

Область определения и область значений квадратичной функции:
Область определения квадратичной функции - это множество всех действительных чисел, поскольку функция определена для всех значений \(x\). Область значений зависит от знака ведущего коэффициента \(a\). Если \(a>0\), область значений - это \( \left [k, \infty \right ) \), и если \(a < 0 \), область значений - \( \left ( - \infty ,k \right ] \).

График:
График квадратичной функции может быть преобразован изменением значений \(a\), \(b\) и \(c\). Например, если \(a\) умножается на положительную константу, график растягивается вертикально, а если \(a\) умножается на отрицательную константу, график отражается относительно оси \(x\). Если к \(x\) добавляется или вычитается \(b\), график сдвигается горизонтально, и если к \(f(x)\) добавляется или вычитается \(c\), график сдвигается вертикально.

Модульная или Абсолютная функция и её график☰

Функция \( f(x)=|x| \) является кусочно-заданной функцией, которая берет абсолютное значение ввода \(x\). Функция абсолютного значения определяется следующим образом:

\( | x | = \begin{cases} -x & \text{, } x < 0 \\ x & \text{, } x \geq 0 \end{cases} \)

Следовательно, функция \(f(x)=|x|\) принимает значение \(x\), когда \(x\) неотрицательно, и \(-x\), когда \(x\) отрицательно. График \( f(x)=|x| \) представляет собой кривую в форме буквы V с вершиной в начале координат. Наклон кривой меняется при \(x=0\), где функция не является дифференцируемой.

Вот некоторые важные свойства функции абсолютного значения:
Симметрия: Функция \(f(x)=|x|\) симметрична относительно начала координат, что означает, что \(f(x)=f(-x) \) для всех \(x\).

Неотрицательные значения: Абсолютное значение любого вещественного числа неотрицательно, что означает, что \( |x| \ge 0 \) для всех \(x\).

Расстояние: Абсолютное значение числа представляет собой его расстояние от нуля на числовой прямой. Например, \(|3|=3\) и \(|-5|=5\).

Кусочно-заданная функция: Функция абсолютного значения является кусочно-заданной функцией, что означает, что она определяется по-разному для различных интервалов ввода \(x\). В частности, \(f(x)=x\), когда \(x \ge 0 \), и \( f(x)=-x \), когда \(x < 0 \).

Применения: Функция абсолютного значения используется в различных приложениях, таких как измерение разницы между двумя значениями, вычисление расстояний и решение уравнений абсолютного значения.

График:

В заключение, функция абсолютного значения является кусочно-заданной функцией, которая принимает неотрицательное значение своего входа, если он неотрицателен, и отрицательное значение своего входа, если он отрицателен. График \(f(x)=|x| \) представляет собой кривую в форме буквы V, которая симметрична относительно начала координат.

Кубическая функция и её график ☰

Функция \(f(x)=x^3\) является кубической функцией, которая берет входное значение \(x\) и возводит его в третью степень. График \(f(x)=x^3 \) является кривой, проходящей через начало координат и имеющей форму, схожую с буквой "S". Функция определена для всех действительных значений \(x\).

Вот некоторые важные свойства кубической функции:
Область и область значений: Область функции \(f(x)=x^3 \) - все действительные числа, что означает, что в функцию можно подставить любое действительное число. Область значений функции также является всеми действительными числами, что означает, что выходные данные могут принимать любые действительные значения.

Симметрия: Функция \(f(x)=x^3 \) является нечетной функцией, что означает, что \(f(-x)=-f(x) \) для всех \(x\). Это свойство приводит к тому, что график функции симметричен относительно начала координат.

Перехваты: Функция \(f(x)=x^3 \) проходит через начало координат, что означает, что у нее есть \(y\)-перехват равный нулю. У функции нет никаких \(x\)-перехватов.

Интервалы возрастания и убывания: Функция \(f(x)=x^3 \) возрастает для всех \(x\), что означает, что значение функции увеличивается по мере увеличения \(x\). Это свойство приводит к тому, что график функции направлен вверх. У функции нет локальных максимумов или минимумов.

Применение: Кубическая функция используется в различных приложениях, таких как моделирование объема куба или рост населения.

График


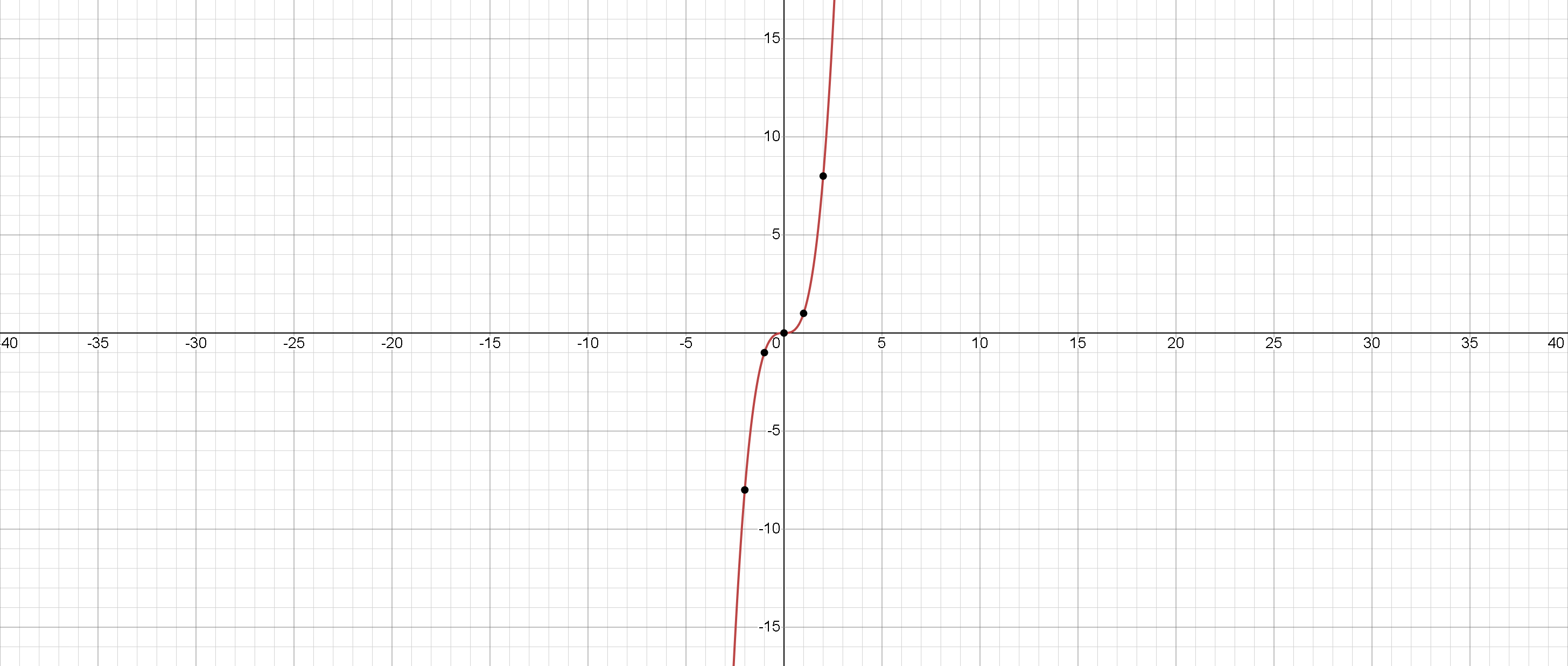
В заключение, кубическая функция \(f(x)=x^3 \) - это функция, которая возводит входное значение \(x\) в третью степень. График функции представляет собой кривую, направленную вверх, которая проходит через начало координат и симметрична относительно начала координат. Функция определена для всех действительных значений \(x\) и имеет область значений всех действительных чисел.