Polígonos ☰

Un polígono es una figura geométrica bidimensional que consta de un número finito de segmentos de recta (llamados lados o aristas) que están conectados extremo a extremo para formar una forma cerrada. La palabra "polígono" proviene de las palabras griegas "poly" (que significa "muchos") y "gon" (que significa "ángulo").
Los polígonos pueden tener cualquier número de lados, pero deben ser líneas rectas y no pueden intersectarse. Los polígonos con tres lados se llaman triángulos, los polígonos con cuatro lados se llaman cuadriláteros, los polígonos con cinco lados se llaman pentágonos, y así sucesivamente.
El perímetro de un polígono es la suma de las longitudes de sus lados. Si un polígono tiene \(n\) lados y la longitud de cada lado se denota por \(s_i\) para \(i = 1,2,…,n,\) entonces el perímetro \(P\) está dado por:
\( P = s_1 + s_2 + \ldots + s_n = \sum_{i=1}^n s_i\)

Los ángulos interiores de un polígono son los ángulos formados por dos lados adyacentes dentro del polígono. La suma de los ángulos interiores de un polígono con \(n\) lados está dada por la fórmula:
\( \sum_{i=1}^n \theta_i =(n-2) \cdot 180^\circ \) , donde \( \theta_i \) es la medida del \(i-ésimo\) ángulo interior en grados.

Polígonos regulares son polígonos en los que todos los lados tienen la misma longitud y todos los ángulos interiores tienen la misma medida. La medida de cada ángulo interior de un polígono regular con \(n\) lados está dada por:
\( \theta = \frac{(n-2) \cdot 180^\circ }{n} \) .

El área de un polígono se puede calcular de varias maneras, dependiendo de la forma del polígono.
Por ejemplo, el área de un triángulo se puede calcular utilizando la fórmula: \( A = \frac{1}{2} bh \) , donde \(b\) es la base del triángulo y \(h\) es su altura.
El área de un polígono regular con \(n\) lados y longitud de lado \(s\) se puede calcular utilizando la fórmula: \( A= \frac{1}{4} ns^2 cot(\frac{\pi }{n}) \), donde \(cot(x)\) es la función cotangente.

Los polígonos se utilizan en muchos campos diferentes, incluyendo matemáticas, ingeniería y gráficos por computadora. También se utilizan en la vida cotidiana, como en el diseño de edificios y muebles.

Polígonos convexos y cóncavos ☰

Los polígonos pueden clasificarse como convexos o cóncavos según la naturaleza de sus ángulos.
Un polígono convexo es un polígono en el que todos sus ángulos interiores son menores que 180 grados. En otras palabras, si trazas un segmento de línea recta entre cualquier par de puntos dentro del polígono, el segmento siempre estará completamente dentro del polígono. De manera equivalente, un polígono convexo es un polígono que no "se dobla hacia adentro" como una cuchara.
Ejemplos de polígonos convexos incluyen triángulos equiláteros, cuadrados, pentágonos regulares y hexágonos regulares. Los polígonos convexos son importantes en muchas áreas de las matemáticas y aplicaciones, ya que tienen muchas propiedades útiles y son relativamente fáciles de trabajar.
Por otro lado, un polígono cóncavo es un polígono en el que al menos uno de sus ángulos interiores es mayor que 180 grados. En otras palabras, si trazas un segmento de línea recta entre cualquier par de puntos dentro del polígono, el segmento cruzará el límite del polígono. De manera equivalente, un polígono cóncavo es un polígono que "se dobla hacia adentro" como una cuchara.
Ejemplos de polígonos cóncavos incluyen la letra "C" (cuando se dibuja como una forma cerrada), la letra "L" y cualquier polígono con una "muesca" o "diente" en su límite. Los polígonos cóncavos son menos comunes en aplicaciones, ya que tienen geometría más complicada y pueden ser más difíciles de trabajar matemáticamente.
Una diferencia importante entre los polígonos convexos y cóncavos es que los polígonos convexos tienen un punto central único llamado centroide, que también es el centro de balance o gravedad del polígono. Esto hace que los polígonos convexos sean útiles en aplicaciones como ingeniería y arquitectura, donde el equilibrio y la estabilidad son factores importantes. Por otro lado, los polígonos cóncavos no tienen un centroide único, lo que los hace más difíciles de analizar y trabajar.

La suma de los ángulos interiores de un polígono convexo ☰

La suma de los ángulos interiores de un polígono convexo con \(n\) lados se da mediante la fórmula: \( \sum_{i=1}^n \theta_i =(n-2)⋅180^\circ \), donde \( \theta_i\) es la medida del \(i-ésimo\) ángulo interior en grados.
La suma de los ángulos exteriores de un polígono convexo siempre es de 360 grados, independientemente del número de lados. Esto significa que si mides cada ángulo exterior de un polígono convexo y sumas las medidas, el total siempre será de 360 grados.
Para ver por qué esto es cierto, imagina caminar alrededor del perímetro del polígono y girar en cada vértice para seguir el siguiente lado. En cada giro, estás formando un ángulo exterior con el lado que acabas de dejar. Si das una vuelta completa alrededor del polígono, habrás girado un total de 360 grados.
Podemos usar la fórmula de la suma de los ángulos interiores y el hecho de que los ángulos exteriores suman 360 grados para encontrar la medida de cada ángulo exterior. Sea \(a_i\) la medida del \(i-ésimo\) ángulo exterior en grados. Entonces tenemos:

\( \sum_{i=1}^n \theta_i + \sum_{i=1}^n a_i =(n-2) \cdot 180^\circ +360^\circ \)

\( \small \sum_{i=1}^n a_i =(\sum_{i=1}^n \theta_i )-(n-2) \cdot 180^\circ +360^\circ = \) \( (n-2) \cdot 180^\circ -(n-2) \cdot 180^\circ +360^\circ=360^\circ \)

Por lo tanto, la medida de cada ángulo exterior de un polígono convexo se da por: \( a_i= 360^\circ - \theta_i \).
Ten en cuenta que esta fórmula se aplica solo a polígonos convexos, y no a polígonos cóncavos, que pueden tener ángulos exteriores mayores que 180 grados.

Polígono inscrito y circunscrito ☰

Los polígonos inscritos y circunscritos son conceptos importantes en geometría que implican polígonos inscritos dentro y circunscritos alrededor de un círculo. Estos conceptos se utilizan a menudo en diversas áreas de las matemáticas, como la geometría, la trigonometría y el cálculo.

Polígono inscrito
Un polígono inscrito es un polígono que se dibuja dentro de un círculo de modo que todos sus vértices yacen en la circunferencia del círculo. La figura siguiente muestra un ejemplo de un polígono inscrito.


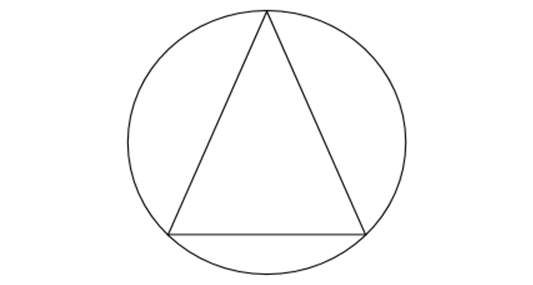
La propiedad clave de un polígono inscrito es que la suma de los ángulos interiores es igual a \( (n-2) 180^\circ \), donde \(n\) es el número de lados del polígono. Esto se conoce como la suma de los ángulos interiores de un polígono. Podemos demostrar esta propiedad utilizando el hecho de que el ángulo central del círculo subtiende cada lado del polígono es igual al ángulo interior correspondiente del polígono. Dado que la suma de los ángulos centrales es \( 360^\circ \) (el ángulo completo del círculo), la suma de los ángulos interiores debe ser \( (n-2) 180^\circ \).
Otra propiedad importante de un polígono inscrito es que el producto de las longitudes de sus lados se maximiza cuando el polígono es un polígono regular. Es decir, si \(s_1\), \(s_2\), … , \(s_n\) son las longitudes de los lados de un polígono inscrito con \(n\) lados, entonces el producto \(s_1\), \(s_2\), … , \(s_n\) se maximiza cuando el polígono es un polígono regular.

Polígono circunscrito
Un polígono circunscrito es un polígono que se dibuja fuera de un círculo de modo que todos sus vértices yacen en la circunferencia del círculo. La figura siguiente muestra un ejemplo de un polígono circunscrito.


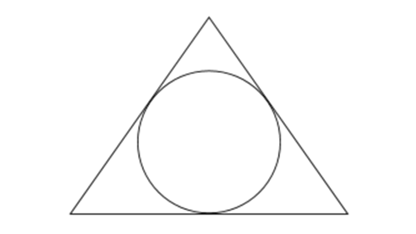
La propiedad clave de un polígono circunscrito es que el producto de las longitudes de sus lados es igual a \( 2R^n \sin( \frac{360^\circ}{n} ) \), donde \(n\) es el número de lados del polígono y \(R\) es el radio del círculo. Esto se conoce como la fórmula del producto de los lados de un polígono. Podemos demostrar esta fórmula utilizando el hecho de que la longitud de cada lado del polígono es igual a dos veces el radio por el seno de la mitad del ángulo central del círculo subtiende por ese lado. Dado que el ángulo central de un polígono regular con \(n\) lados es \( \frac{360^\circ}{n} \), tenemos la fórmula anterior.
Otra propiedad importante de un polígono circunscrito es que el área del polígono se maximiza cuando el polígono es un polígono regular. Es decir, si \(A\) es el área de un polígono circunscrito con \(n\) lados, entonces el área se maximiza cuando el polígono es un polígono regular.

Ejemplos
Consideremos un ejemplo para ilustrar estos conceptos. Supongamos que tenemos un círculo con radio 5. ¿Cuál es el área máxima de un pentágono inscrito (un polígono con cinco lados) en este círculo, y cuál es el área máxima de un pentágono circunscrito?

Para encontrar el área máxima de un pentágono inscrito, necesitamos encontrar la longitud del lado que maximiza el producto de las longitudes de los lados. Dado que el pentágono está inscrito en un círculo de radio 5, la longitud del lado se da por \(s =2R \sin(\frac{180^\circ}{5} ) = 2 \cdot 5\sin(36^\circ )= 6.472 \). Por lo tanto, el área máxima de un pentágono inscrito se alcanza cuando el pentágono es regular, y se da por:
\( A_\text{inscrito} = \frac{5s^2}{4} \cdot \tan(36^\circ ) \approx 61.937\)

Para encontrar el área máxima de un pentágono circunscrito, podemos usar la fórmula del producto de los lados de un polígono. Para un pentágono, tenemos:
\( \small A_\text{circunscrito} =\frac{5s^2}{4} \cdot \cot(36^\circ )=5R^2 \sin(72^\circ ) \approx 78.589\)

Nuevamente, el área máxima de un pentágono circunscrito se alcanza cuando el pentágono es regular.

En resumen, los polígonos inscritos y circunscritos son conceptos importantes en geometría que involucran polígonos inscritos dentro y circunscritos alrededor de un círculo. Estos conceptos tienen muchas propiedades interesantes y se utilizan en diversas áreas de las matemáticas.

Círculos dibujados dentro y fuera de un triángulo ☰

El tema de los círculos dibujados dentro y fuera de un triángulo es un aspecto importante de la geometría elemental. Hay varios teoremas relacionados con los círculos dibujados dentro y fuera de un triángulo, que se discuten a continuación:

Círculo inscrito e incenter:
Un círculo inscrito en un triángulo es un círculo que es tangente a los tres lados del triángulo. El centro del círculo inscrito se llama el incentro del triángulo. El incentro está equidistante de los tres lados del triángulo.

Teorema 1: El incentro de un triángulo es la intersección de sus tres bisectrices de ángulo.

Prueba: Sea ABC un triángulo, y sea I el centro de su círculo inscrito. Sea D, E, y F los puntos donde el círculo inscrito es tangente a los lados BC, AC, y AB, respectivamente. Entonces, ID, IE, y IF son los bisectores perpendiculares de EF, FD, y DE, respectivamente. Por lo tanto, ID es el bisector del ángulo BIC, donde B y C son los vértices del triángulo, y I es el incentro. De manera similar, IE e IF son los bisectores del ángulo AIC y AIB, respectivamente. Por lo tanto, las tres bisectrices de ángulo del triángulo se intersecan en el incentro I.

Teorema 2: La distancia desde el incentro de un triángulo a cualquier lado del triángulo es igual al radio del círculo inscrito.

Prueba: Sea ABC un triángulo, y sea I el centro de su círculo inscrito. Sea D, E, y F los puntos donde el círculo inscrito es tangente a los lados BC, AC, y AB, respectivamente. Entonces, ID, IE, y IF son los bisectores perpendiculares de EF, FD, y DE, respectivamente. Por lo tanto, ID es la altura del triángulo IBC desde el vértice I hasta el lado BC. De manera similar, IE e IF son las alturas de los triángulos AIC y AIB desde el vértice I hasta los lados AC y AB, respectivamente. Dado que \(ID=IE=IF\), se sigue que la distancia desde el incentro I a cualquier lado del triángulo es igual al radio del círculo inscrito.

Circuncírculo y Centro circunscrito:
Un circuncírculo de un triángulo es un círculo que pasa por los tres vértices del triángulo. El centro del circuncírculo se llama el centro circunscrito del triángulo. El centro circunscrito es la intersección de los bisectores perpendiculares de los lados del triángulo.

Teorema 3: El centro circunscrito de un triángulo es la intersección de los bisectores perpendiculares de sus lados.

Prueba: Sea ABC un triángulo, y sea O el centro de su circuncírculo. Sea D, E, y F los puntos medios de los lados BC, AC, y AB, respectivamente. Entonces, OD, OE, y OF son los bisectores perpendiculares de los lados BC, AC, y AB, respectivamente. Por lo tanto, OD es perpendicular a BC, y \(OD=\frac{1}{2} BC\). De manera similar, OE es perpendicular a AC, y \(OE=\frac{1}{2} AC\). De manera similar, OF es perpendicular a AB, y \( OF= \frac{1}{2} AB \). Por lo tanto, O está equidistante de todos los tres vértices del triángulo y por lo tanto, se encuentra en los bisectores perpendiculares de los tres lados. Por lo tanto, el centro circunscrito del triángulo es la intersección de los bisectores perpendiculares de sus lados.

Teorema 4: Los bisectores perpendiculares de los lados de un triángulo son concurrentes si y solo si el triángulo es agudo, recto u obtuso.

Prueba: Sea ABC un triángulo, y sea D, E, y F los puntos medios de los lados BC, AC, y AB, respectivamente. Supongamos que los bisectores perpendiculares de los lados BC, AC, y AB son concurrentes en un punto O. Entonces, \(OD=OE=OF\), y por lo tanto, O está equidistante de todos los tres vértices del triángulo. Por lo tanto, \(OA=OB=OC\), y O es el centro circunscrito del triángulo. Si el triángulo es agudo, entonces el centro circunscrito está dentro del triángulo. Si el triángulo es recto, entonces el centro circunscrito está en el punto medio de la hipotenusa. Si el triángulo es obtuso, entonces el centro circunscrito está fuera del triángulo.

A la inversa, supongamos que el triángulo es agudo, recto u obtuso. Si el triángulo es agudo, entonces los bisectores perpendiculares de los lados se intersectan dentro del triángulo. Si el triángulo es recto, entonces los bisectores perpendiculares de los lados se intersectan en el punto medio de la hipotenusa. Si el triángulo es obtuso, entonces los bisectores perpendiculares de los lados se intersectan fuera del triángulo. Por lo tanto, los bisectores perpendiculares de los lados son concurrentes si y solo si el triángulo es agudo, recto u obtuso.

Excírculos y Excentros:
Un excírculo de un triángulo es un círculo que es tangente a uno de los lados del triángulo y a las extensiones de los otros dos lados. Hay tres excírculos de un triángulo, uno para cada lado. El centro de un excírculo se llama el excentro del triángulo correspondiente a ese lado. El excentro se encuentra en el bisector del ángulo exterior en el vértice opuesto al lado tangente al excírculo.

Teorema 5: El excentro de un triángulo correspondiente a un lado dado se encuentra en el bisector del ángulo exterior en el vértice opuesto a ese lado.

Prueba: Sea ABC un triángulo, y sea \(I_A\) el centro del excírculo correspondiente al lado BC. Sea D el punto de tangencia del excírculo con el lado BC, y sea E y F los puntos de tangencia con los lados CA y AB, respectivamente. Entonces, \(I_A D\) es perpendicular a BC, y \(I_A E\) y \(I_A F\) son los bisectores de los ángulos BAC y CAB, respectivamente. Por lo tanto, \(I_A\) se encuentra en el bisector del ángulo exterior en el vértice A. De manera similar, el excentro \(I_B\) correspondiente al lado AC se encuentra en el bisector del ángulo exterior en el vértice B, y el excentro \(I_C\) correspondiente al lado AB se encuentra en el bisector del ángulo exterior en el vértice C.

En conclusión, el tema de los círculos dibujados dentro y fuera de un triángulo es un aspecto importante de la geometría elemental. Los teoremas relacionados con incírculos, circuncírculos y excírculos son resultados fundamentales que proporcionan valiosas ideas sobre las propiedades de los triángulos.

Propiedades de un cuadrilátero inscrito y circunscrito en un círculo ☰

Se dice que un cuadrilátero está inscrito en un círculo si todos sus vértices están en el círculo. De manera similar, un cuadrilátero está circunscrito alrededor de un círculo si el círculo es tangente a los cuatro lados del cuadrilátero.

Propiedades de un Cuadrilátero Inscrito en un Círculo:

• Los ángulos opuestos de un cuadrilátero inscrito en un círculo son suplementarios. Es decir, la suma de las medidas de cualquier par de ángulos opuestos es de 180 grados.
• Las diagonales de un cuadrilátero inscrito en un círculo se intersecan en ángulos rectos. Es decir, las diagonales son perpendiculares entre sí.
• El producto de las longitudes de las dos diagonales de un cuadrilátero inscrito en un círculo es igual a la suma de los productos de las longitudes de los pares de lados opuestos. Es decir, si \(ABCD\) es un cuadrilátero inscrito en un círculo, entonces \(AC \cdot BD=AB \cdot CD+AD \cdot BC\).
• Los segmentos de línea que unen los puntos medios de los lados opuestos de un cuadrilátero inscrito en un círculo son concurrentes. Es decir, los segmentos de línea AC y BD se encuentran en un punto P, donde P es el punto medio de EF y EF es el segmento de línea que une los puntos medios de AB y CD.

Propiedades de un Cuadrilátero Circunscrito alrededor de un Círculo:

• Los lados opuestos de un cuadrilátero circunscrito alrededor de un círculo son paralelos. Es decir,
  \(AB \parallel CD\) y \( AD \parallel BC\).
• La suma de los pares opuestos de lados de un cuadrilátero circunscrito alrededor de un círculo es igual al diámetro del círculo.
  Es decir, \(AB+CD=AD+BC\).
• Los segmentos de línea que unen los puntos de contacto del círculo con los lados de un cuadrilátero circunscrito alrededor de un círculo son concurrentes. Es decir, los segmentos de línea AC y BD se encuentran en un punto P, donde P es la intersección de las tangentes al círculo en B y D.
• El área de un cuadrilátero circunscrito alrededor de un círculo se puede calcular utilizando la fórmula de Brahmagupta:
  \( \text{Área} =\sqrt{(s-a)(s-b)(s-c)(s-d)} \), donde \(a\), \(b\), \(c\) y \(d\) son las longitudes de los lados del cuadrilátero y \(s\) es el semiperímetro, dado por: \(s=\frac{a+b+c+d}{2} \).
• Si un cuadrilátero está tanto inscrito como circunscrito alrededor de un círculo, entonces debe ser un cuadrado. En otras palabras, si un cuadrilátero tiene la propiedad de que sus vértices están en un círculo y el círculo es tangente a los cuatro lados del cuadrilátero, entonces el cuadrilátero debe ser un cuadrado.

Círculos dentro y fuera de un polígono regular ☰

Un polígono regular es un polígono con todos los lados y ángulos iguales. Se pueden inscribir círculos dentro y circunscribir círculos alrededor de un polígono regular.

Círculo Inscrito en un Polígono Regular:
Un círculo inscrito en un polígono regular toca cada lado del polígono en un solo punto. El centro del círculo también es el centro del polígono.
Sea \(r\) el radio del círculo inscrito, \(s\) la longitud de un lado del polígono regular y \(n\) el número de lados del polígono.
El área \(A\) del polígono regular se puede calcular utilizando la fórmula: \( A=\frac{1}{2} nr^2 sin \frac{2 \pi }{n} \).

El perímetro \(P\) del polígono regular se calcula mediante: \(P=ns\).
El radio \(r\) del círculo inscrito se puede calcular utilizando la fórmula: \( r= \frac{s}{2 tan \frac{\pi}{n}} \)

Círculo Circunscrito alrededor de un Polígono Regular:
Un círculo circunscrito alrededor de un polígono regular pasa por cada vértice del polígono. El centro del círculo también es el centro del polígono.
Sea \(R\) el radio del círculo circunscrito, \(s\) la longitud de un lado del polígono regular y \(n\) el número de lados del polígono.
El área \(A\) del polígono regular se puede calcular utilizando la fórmula: \( A=\frac{1}{2} nR^2 sin \frac{2 \pi }{n} \).

El perímetro \(P\) del polígono regular se calcula mediante: \(P = ns\).
El radio \(R\) del círculo circunscrito se puede calcular utilizando la fórmula: \( R= \frac{s}{2 sin \frac{\pi}{n}} \)

Además, la razón del área del círculo circunscrito al área del círculo inscrito está dada por:
\( \frac{\text{Área del Círculo Circunscrito}}{ \text{Área del Círculo Inscrito}} = \frac{R^2}{r^2} = \frac{sin^2 \frac{\pi}{n}}{1- sin^2 \frac{\pi}{n}} \)

Área de un polígono. Área del polígono regular. ☰

El área de un polígono es la medida de la región bidimensional encerrada por el polígono. La fórmula para encontrar el área de un polígono depende del tipo de polígono.
Por ejemplo, el área de un triángulo se puede calcular utilizando la fórmula:
\( \text{Área del Triángulo} = \frac{1}{2} \cdot \text{base} \cdot \text{altura} \)

Para un rectángulo, el área se puede calcular utilizando la fórmula:
\( \text{Área del Rectángulo} = \text{largo} \cdot \text{ancho} \)

Para polígonos irregulares, existen diferentes métodos para calcular el área, como descomponerlo en formas más simples y sumar las áreas o utilizando cálculo.

Por otro lado, el área de un polígono regular se puede calcular utilizando la siguiente fórmula:
\( \small \text{Área del Polígono Regular} = \frac{1}{2} \cdot \text{Perímetro} \cdot \text{Apotema} \). Donde el Perímetro es la suma de las longitudes de todos los lados del polígono, y la Apotema es la distancia perpendicular desde el centro del polígono hasta uno de sus lados.

El polígono regular es un polígono que tiene todos los lados de la misma longitud y todos los ángulos de igual medida. Ejemplos de polígonos regulares incluyen triángulos equiláteros, cuadrados, pentágonos regulares, hexágonos, y así sucesivamente.