Polygons ☰

A polygon is a two-dimensional geometric figure that consists of a finite number of line segments (called sides or edges) that are connected end-to-end to form a closed shape. The word "polygon" comes from the Greek words "poly" (meaning "many") and "gon" (meaning "angle").
Polygons can have any number of sides, but they must be straight lines and cannot intersect. Polygons with three sides are called triangles, polygons with four sides are called quadrilaterals, polygons with five sides are called pentagons, and so on.
The perimeter of a polygon is the sum of the lengths of its sides. If a polygon has \(n\) sides and the length of each side is denoted by \(s_i\) for \(i = 1,2,…,n,\) then the perimeter \(P\) is given by:
\( P = s_1 + s_2 + \ldots + s_n = \sum_{i=1}^n s_i\)

The interior angles of a polygon are the angles formed by any two adjacent sides inside the polygon. The sum of the interior angles of a polygon with \(n\) sides is given by the formula:
\( \sum_{i=1}^n \theta_i =(n-2) \cdot 180^\circ \) , where \( \theta_i \) is the measure of the \(i-th\) interior angle in degrees.

Regular polygons are polygons in which all sides have the same length and all interior angles have the same measure. The measure of each interior angle of a regular polygon with \(n\) sides is given by:
\( \theta = \frac{(n-2) \cdot 180^\circ }{n} \) .

The area of a polygon can be calculated in several ways, depending on the shape of the polygon.
For example, the area of a triangle can be calculated using the formula: \( A = \frac{1}{2} bh \) , where \(b\) is the base of the triangle and \(h\) is its height.
The area of a regular polygon with \(n\) sides and side length \(s\) can be calculated using the formula: \( A= \frac{1}{4} ns^2 cot(\frac{\pi }{n}) \), where \(cot(x)\) is the cotangent function.

Polygons are used in many different fields, including mathematics, engineering, and computer graphics. They are also used in everyday life, such as in the design of buildings and furniture.

Convex and concave polygons. ☰

Polygons can be classified as convex or concave based on the nature of their angles.
A convex polygon is a polygon in which all of its interior angles are less than 180 degrees. In other words, if you draw a straight line segment between any two points inside the polygon, the segment will always lie entirely within the polygon. Equivalently, a convex polygon is a polygon that does not "bend inward" like a spoon.
Examples of convex polygons include equilateral triangles, squares, regular pentagons, and regular hexagons. Convex polygons are important in many areas of mathematics and applications, as they have many useful properties and are relatively easy to work with.
On the other hand, a concave polygon is a polygon in which at least one of its interior angles is greater than 180 degrees. In other words, if you draw a straight line segment between any two points inside the polygon, the segment will cross the boundary of the polygon. Equivalently, a concave polygon is a polygon that "bends inward" like a spoon.
Examples of concave polygons include the letter "C" (when drawn as a closed shape), the letter "L", and any polygon with a "notch" or "dent" in its boundary. Concave polygons are less common in applications, as they have more complicated geometry and can be more difficult to work with mathematically.
One important difference between convex and concave polygons is that convex polygons have a unique center point called the centroid, which is also the center of balance or gravity of the polygon. This makes convex polygons useful in applications such as engineering and architecture, where balance and stability are important factors. On the other hand, concave polygons do not have a unique centroid, which makes them more difficult to analyze and work with.

The sum of the interior angles of a convex polygon ☰

The sum of the interior angles of a convex polygon with \(n\) sides is given by the formula: \( \sum_{i=1}^n \theta_i =(n-2)⋅180^\circ \), where \( \theta_i\) is the measure of the \(i-th\) interior angle in degrees.
The sum of the exterior angles of a convex polygon is always 360 degrees, regardless of the number of sides. This means that if you measure each exterior angle of a convex polygon and add up the measures, the total will always be 360 degrees.
To see why this is true, imagine walking around the perimeter of the polygon and turning at each vertex to follow the next side. At each turn, you are making an exterior angle with the side you just left. If you make a full circuit around the polygon, you will have turned a total of 360 degrees.
We can use the sum of the interior angles formula and the fact that the exterior angles add up to 360 degrees to find the measure of each exterior angle. Let \(a_i\) be the measure of the \(i-th\) exterior angle in degrees. Then we have:

\( \sum_{i=1}^n \theta_i + \sum_{i=1}^n a_i =(n-2) \cdot 180^\circ +360^\circ \)

\( \small \sum_{i=1}^n a_i =(\sum_{i=1}^n \theta_i )-(n-2) \cdot 180^\circ +360^\circ = \) \( (n-2) \cdot 180^\circ -(n-2) \cdot 180^\circ +360^\circ=360^\circ \)

Therefore, the measure of each exterior angle of a convex polygon is given by: \( a_i= 360^\circ - \theta_i \).
Note that this formula applies only to convex polygons, and not to concave polygons, which can have exterior angles that are greater than 180 degrees.

Inscribed and circumscribed polygon ☰

Inscribed and circumscribed polygons are important concepts in geometry that involve polygons inscribed within and circumscribed around a circle. These concepts are often used in various areas of mathematics, such as geometry, trigonometry, and calculus.

Inscribed Polygon
An inscribed polygon is a polygon that is drawn inside a circle such that all its vertices lie on the circumference of the circle. The figure below shows an example of an inscribed polygon.


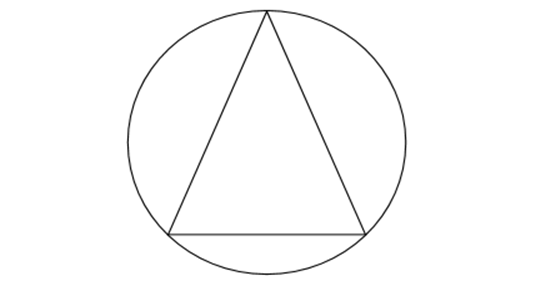
The key property of an inscribed polygon is that the sum of the interior angles is equal to \( (n-2) 180^\circ \), where \(n\) is the number of sides of the polygon. This is known as the interior angle sum of a polygon. We can prove this property using the fact that the central angle of the circle subtended by each side of the polygon is equal to the corresponding interior angle of the polygon. Since the sum of the central angles is \( 360^\circ \) (the full angle of the circle), the sum of the interior angles must be \( (n-2) 180^\circ \).
Another important property of an inscribed polygon is that the product of the lengths of its sides is maximized when the polygon is a regular polygon. That is, if \(s_1\), \(s_2\), … , \(s_n\) are the lengths of the sides of an inscribed polygon with \(n\) sides, then the product \(s_1\), \(s_2\), … , \(s_n\) is maximized when the polygon is a regular polygon.

Circumscribed polygon
A circumscribed polygon is a polygon that is drawn outside a circle such that all its vertices lie on the circumference of the circle. The figure below shows an example of a circumscribed polygon.


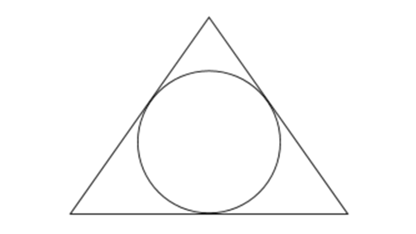
The key property of a circumscribed polygon is that the product of the lengths of its sides is equal to \( 2R^n sin( \frac{360^\circ}{n} ) \) , where \(n\) is the number of sides of the polygon and \(R\) is the radius of the circle. This is known as the product of the sides of a polygon formula. We can prove this formula using the fact that the length of each side of the polygon is equal to twice the radius times the sine of half the central angle of the circle subtended by that side. Since the central angle of a regular polygon with \(n\) sides is \( \frac{360^\circ}{n} \) , we have the formula above.
Another important property of a circumscribed polygon is that the area of the polygon is maximized when the polygon is a regular polygon. That is, if \(A\) is the area of a circumscribed polygon with \(n\) sides, then the area is maximized when the polygon is a regular polygon.

Examples
Let's consider an example to illustrate these concepts. Suppose we have a circle with radius 5. What is the maximum area of an inscribed pentagon (a polygon with five sides) in this circle, and what is the maximum area of a circumscribed pentagon?

To find the maximum area of an inscribed pentagon, we need to find the side length that maximizes the product of the side lengths. Since the pentagon is inscribed in a circle of radius 5, the side length is given by \(s =2R sin(\frac{180^\circ}{5} ) = 2 \cdot 5sin(36^\circ )= 6.472 \) . Therefore, the maximum area of an inscribed pentagon is achieved when the pentagon is regular, and is given by:
\( A_\text{inscribed} = \frac{5s^2}{4} \cdot tan(36^\circ ) \approx 61.937\)

To find the maximum area of a circumscribed pentagon, we can use the product of the sides of a polygon formula. For a pentagon, we have:
\( \small A_\text{circumscribed} =\frac{5s^2}{4} \cdot cot(36^\circ )=5R^2 sin(72^\circ ) \approx 78.589\)

Again, the maximum area of a circumscribed pentagon is achieved when the pentagon is regular.

In summary, inscribed and circumscribed polygons are important concepts in geometry that involve polygons inscribed within and circumscribed around a circle. These concepts have many interesting properties and are used in various areas of mathematics.

Circles drawn inside and outside a triangle ☰

The topic of circles drawn inside and outside a triangle is an important aspect of elementary geometry. There are various theorems related to circles drawn inside and outside a triangle, which are discussed below:

Incircle and Incenter:
An incircle of a triangle is a circle that is tangent to all three sides of the triangle. The center of the incircle is called the incenter of the triangle. The incenter is equidistant from all three sides of the triangle.

Theorem 1: The incenter of a triangle is the intersection of its three angle bisectors.

Proof: Let ABC be a triangle, and let I be the center of its incircle. Let D, E, and F be the points where the incircle is tangent to sides BC, AC, and AB, respectively. Then, ID, IE, and IF are the perpendicular bisectors of EF, FD, and DE, respectively. Therefore, ID is the angle bisector of angle BIC, where B and C are the vertices of the triangle, and I is the incenter. Similarly, IE and IF are the angle bisectors of angles AIC and AIB, respectively. Therefore, the three angle bisectors of the triangle intersect at the incenter I.

Theorem 2: The distance from the incenter of a triangle to any side of the triangle is equal to the radius of the incircle.

Proof: Let ABC be a triangle, and let I be the center of its incircle. Let D, E, and F be the points where the incircle is tangent to sides BC, AC, and AB, respectively. Then, ID, IE, and IF are the perpendicular bisectors of EF, FD, and DE, respectively. Therefore, ID is the height of triangle IBC from vertex I to side BC. Similarly, IE and IF are the heights of triangles AIC and AIB from vertex I to sides AC and AB, respectively. Since \(ID=IE=IF\), it follows that the distance from the incenter I to any side of the triangle is equal to the radius of the incircle.

Circumcircle and Circumcenter:
A circumcircle of a triangle is a circle that passes through all three vertices of the triangle. The center of the circumcircle is called the circumcenter of the triangle. The circumcenter is the intersection of the perpendicular bisectors of the sides of the triangle.

Theorem 3: The circumcenter of a triangle is the intersection of the perpendicular bisectors of its sides.

Proof: Let ABC be a triangle, and let O be the center of its circumcircle. Let D, E, and F be the midpoints of sides BC, AC, and AB, respectively. Then, OD, OE, and OF are the perpendicular bisectors of sides BC, AC, and AB, respectively. Therefore, OD is perpendicular to BC, and \(OD=\frac{1}{2} BC\). Similarly, OE is perpendicular to AC, and \(OE=\frac{1}{2} AC\). Similarly, OF is perpendicular to AB, and \( OF= \frac{1}{2} AB \). Therefore, O is equidistant from all three vertices of the triangle and hence lies on the perpendicular bisectors of all three sides. Therefore, the circumcenter of the triangle is the intersection of the perpendicular bisectors of its sides.

Theorem 4: The perpendicular bisectors of the sides of a triangle are concurrent if and only if the triangle is acute, right, or obtuse.

Proof: Let ABC be a triangle, and let D, E, and F be the midpoints of sides BC, AC, and AB, respectively. Suppose that the perpendicular bisectors of sides BC, AC, and AB are concurrent at a point O. Then, \(OD=OE=OF\), and hence O is equidistant from all three vertices of the triangle. Therefore, \(OA=OB=OC\), and O is the circumcenter of the triangle. If the triangle is acute, then the circumcenter lies inside the triangle. If the triangle is right, then the circumcenter lies on the midpoint of the hypotenuse. If the triangle is obtuse, then the circumcenter lies outside the triangle.

Conversely, suppose that the triangle is acute, right, or obtuse. If the triangle is acute, then the perpendicular bisectors of the sides intersect inside the triangle. If the triangle is right, then the perpendicular bisectors of the legs intersect at the midpoint of the hypotenuse. If the triangle is obtuse, then the perpendicular bisectors of the sides intersect outside the triangle. Therefore, the perpendicular bisectors of the sides are concurrent if and only if the triangle is acute, right, or obtuse.

Excircles and Excenters:
An excircle of a triangle is a circle that is tangent to one side of the triangle and to the extensions of the other two sides. There are three excircles of a triangle, one for each side. The center of an excircle is called the excenter of the triangle corresponding to that side. The excenter lies on the angle bisector of the exterior angle at the vertex opposite to the side tangent to the excircle.

Theorem 5: The excenter of a triangle corresponding to a given side lies on the angle bisector of the exterior angle at the vertex opposite to that side.

Proof: Let ABC be a triangle, and let \(I_A\) be the center of the excircle corresponding to side BC. Let D be the point of tangency of the excircle with side BC, and let E. And F be the points of tangency with sides CA and AB, respectively. Then, \(I_A D\) is perpendicular to BC, and \(I_A E\) and \(I_A F\) are the angle bisectors of angles BAC and CAB, respectively. Therefore, \(I_A\) lies on the angle bisector of the exterior angle at vertex A. Similarly, the excenter \(I_B\) corresponding to side AC lies on the angle bisector of the exterior angle at vertex B, and the excenter \(I_C\) corresponding to side AB lies on the angle bisector of the exterior angle at vertex C.

In conclusion, the topic of circles drawn inside and outside a triangle is an important aspect of elementary geometry. The theorems related to incircles, circumcircles, and excircles are fundamental results that provide valuable insights into the properties of triangles.

Properties of a quadrilateral inscribed in and outside a circle ☰

A quadrilateral is said to be inscribed in a circle if all its vertices lie on the circle. Similarly, a quadrilateral is said to be circumscribed about a circle if the circle is tangent to all four sides of the quadrilateral.

Properties of a Quadrilateral Inscribed in a Circle:

• The opposite angles of a quadrilateral inscribed in a circle are supplementary. That is, the sum of the measures of any two opposite angles is 180 degrees.
• The diagonals of a quadrilateral inscribed in a circle intersect at right angles. That is, the diagonals are perpendicular to each other.
• The product of the lengths of the two diagonals of a quadrilateral inscribed in a circle is equal to the sum of the products of the lengths of the pairs of opposite sides. That is, if \(ABCD\) is a quadrilateral inscribed in a circle, then \(AC \cdot BD=AB \cdot CD+AD \cdot BC\).
• The line segments joining the midpoints of opposite sides of a quadrilateral inscribed in a circle are concurrent. That is, the line segments AC and BD meet at a point P, where P is the midpoint of EF and EF is the line segment joining the midpoints of AB and CD.

Properties of a Quadrilateral Circumscribed about a Circle:

• The opposite sides of a quadrilateral circumscribed about a circle are parallel. That is,
  \(AB \parallel CD\) and \( AD \parallel BC\).
• The sum of the opposite pairs of sides of a quadrilateral circumscribed about a circle is equal to the diameter of the circle.
  That is, \(AB+CD=AD+BC\).
• The line segments joining the points of contact of the circle with the sides of a quadrilateral circumscribed about a circle are concurrent. That is, the line segments AC and BD meet at a point P, where P is the intersection of the tangents to the circle at B and D.
• The area of a quadrilateral circumscribed about a circle can be calculated using Brahmagupta's formula:
  \( \text{Area} =\sqrt{(s-a)(s-b)(s-c)(s-d)} \), where \(a\), \(b\), \(c\) and \(d\) are the lengths of the sides of the quadrilateral and \(s\) is the semiperimeter, given by: \(s=\frac{a+b+c+d}{2} \).
• If a quadrilateral is both inscribed in and circumscribed about a circle, then it must be a square. In other words, if a quadrilateral has the property that its vertices lie on a circle and the circle is tangent to all four sides of the quadrilateral, then the quadrilateral must be a square.

Circles inside and outside of a regular polygon ☰

A regular polygon is a polygon with all sides and angles equal. Circles can be inscribed inside and circumscribed around a regular polygon.

Circle Inscribed in a Regular Polygon:
A circle inscribed in a regular polygon touches each side of the polygon at a single point. The center of the circle is also the center of the polygon.
Let \(r\) be the radius of the inscribed circle, \(s\) be the length of a side of the regular polygon and \(n\) be the number of sides of the polygon.
The area \(A\) of the regular polygon can be calculated using the formula: \( A=\frac{1}{2} nr^2 sin \frac{2 \pi }{n} \).

The perimeter P of the regular polygon is given by: \(P=ns\).
The radius r of the inscribed circle can be calculated using the formula: \( r= \frac{s}{2 tan \frac{\pi}{n}} \)

Circle Circumscribed around a Regular Polygon:
A circle circumscribed around a regular polygon passes through each vertex of the polygon. The center of the circle is also the center of the polygon.
Let \(R\) be the radius of the circumscribed circle, \(s\) be the length of a side of the regular polygon and \(n\) be the number of sides of the polygon.
The area \(A\) of the regular polygon can be calculated using the formula: \( A=\frac{1}{2} nR^2 sin \frac{2 \pi }{n} \).

The perimeter \(P\) of the regular polygon is given by: \(P = ns\).
The radius \(R\) of the circumscribed circle can be calculated using the formula: \( R= \frac{s}{2 sin \frac{\pi}{n}} \)

In addition, the ratio of the area of the circumscribed circle to the area of the inscribed circle is given by:
\( \frac{\text{Area of Circumscribed Circle}}{ \text{Area of Inscribed Circle}} = \frac{R^2}{r^2} = \frac{sin^2 \frac{\pi}{n}}{1- sin^2 \frac{\pi}{n}} \)

Area of a polygon. Area of the regular polygon ☰

The area of a polygon is the measure of the two-dimensional region enclosed by the polygon. The formula to find the area of a polygon depends on the type of polygon.
For example, the area of a triangle can be calculated using the formula:
\( \text{Area of Triangle} = \frac{1}{2} \cdot \text{base} \cdot \text{height} \)

For a rectangle, the area can be calculated using the formula:
\( \text{Area of Rectangle} = \text{length} \cdot \text{width} \)

For irregular polygons, there are different methods to calculate the area, such as breaking it down into simpler shapes and adding up the areas or using calculus.

On the other hand, the area of a regular polygon can be calculated using the following formula:
\( \small \text{Area of Regular Polygon} = \frac{1}{2} \cdot \text{Perimeter} \cdot \text{Apothem} \). Where Perimeter is the sum of the lengths of all sides of the polygon, and Apothem is the perpendicular distance from the center of the polygon to one of its sides.

The regular polygon is a polygon that has all sides of equal length and all angles of equal measure. Examples of regular polygons include equilateral triangles, squares, regular pentagons, hexagons, and so on.