Cubo ☰

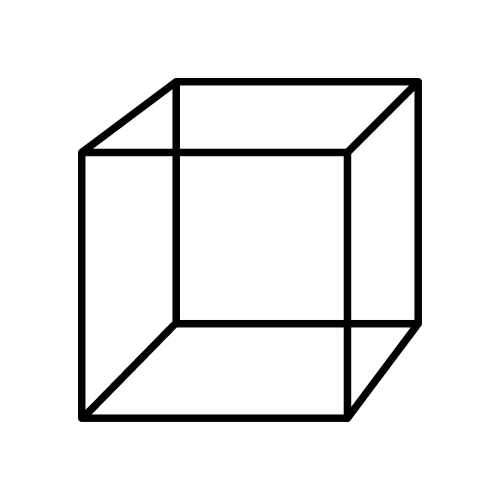
Fórmula del volumen:

\(V=a^3\)

Área superficial del cubo:

\(S=6a^2\)

Área de la superficie lateral del cubo:

\(S=4a^2\)

Diagonal:

\(d= a \sqrt{3}\)

Definición:

Un paralelepípedo rectangular con dimensiones iguales se llama cubo. Tiene 6 caras, cada una en forma de un cuadrado, 12 aristas y 8 puntos de esquina. El número de aristas que emanan de un solo punto es 3.

Paralelepípedo ☰

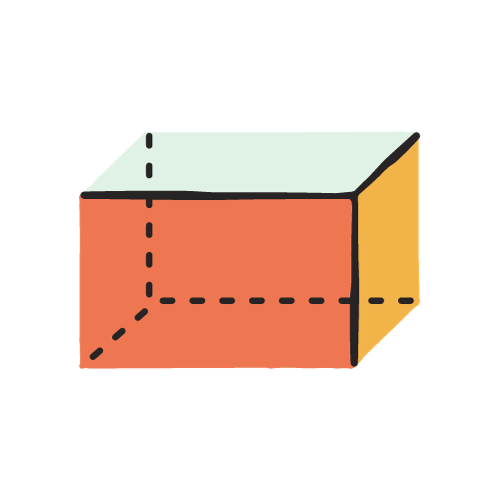
Fórmula del volumen de un paralelepípedo rectangular:

\(V=a \cdot b \cdot c \)

Área superficial total:

\( \small S = 2 \cdot ( a \cdot b + a \cdot c + b \cdot c) \)

Área de la superficie lateral:

\(S = 2 \cdot ( a \cdot c + b \cdot c ) \)

Diagonal:

Para un Rectángulo:

Diagonal (\( \small d\)) = \( \small \sqrt{{\text{Longitud}^2 + \text{Anchura}^2}}\)

Para un Cuadrado:

Diagonal (\( \small d\)) = \( \small \text{Lado} \times \sqrt{2}\)

Para un Paralelogramo:

Diagonal 1 (\( \small d_1\)) = \( \small \text{Lado 1} \times \sqrt{2}\)

Diagonal 2 (\( \small d_2\)) = \( \small \text{Lado 2} \times \sqrt{2}\)

Para un Cubo:

Diagonal (\( \small d \)) = \( \small \text{Lado} \times \sqrt{3}\)

Para una Caja Rectangular (Paralelepípedo Rectangular):

Diagonal (\( \small d\)) = \( \small \sqrt{{\text{Longitud}^2 + \text{Anchura}^2 + \text{Altura}^2}}\)

Para un Rombo:

Diagonal 1 (\( \small d_1\)) = \( \small 2 \times \text{Lado} \times \sin(\frac{\theta}{2})\), donde \(\theta\) es uno de los ángulos.

Diagonal 2 (\( \small d_2\)) = \( \small 2 \times \text{Lado} \times \sin(90^\circ - \frac{\theta}{2})\)

Definición:

Un paralelepípedo es una figura geométrica tridimensional con seis caras en forma de paralelogramos. Es un poliedro, lo que significa que tiene caras planas, aristas rectas y esquinas afiladas (vértices). El término "paralelepípedo" a menudo se utiliza de manera más específica para referirse a un paralelepípedo de seis caras.

Las principales características de un paralelepípedo son las siguientes:

1. Seis Caras: Un paralelepípedo tiene seis caras, que son paralelogramos. Estas caras vienen en pares, donde cada cara es paralela a otra.

2. Aristas: Tiene 12 aristas, que son los segmentos de línea donde se encuentran dos caras.

3. Vértices: Un paralelepípedo tiene 8 vértices, que son los puntos donde se encuentran tres aristas.

4. Caras Opuestas Iguales: Las caras opuestas son iguales en tamaño y forma, y son paralelas entre sí.

5. Ángulos Rectos: Las aristas donde se encuentran las caras forman ángulos rectos.

6. Base Rectangular: En el contexto de un paralelepípedo rectangular, su base consta de cuatro rectángulos congruentes con ángulos rectos.

7. Tres Dimensiones: El paralelepípedo se caracteriza por sus tres dimensiones: longitud, anchura y altura.

Cilindro ☰

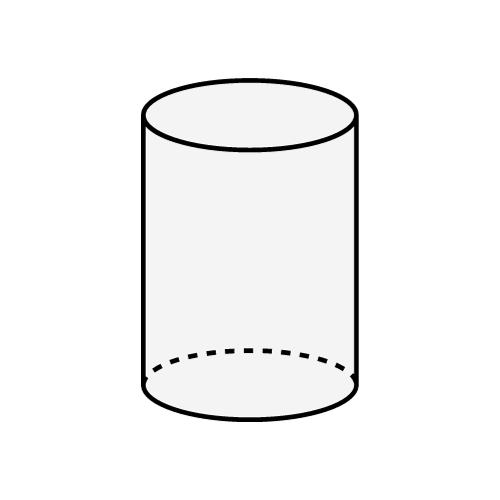
Fórmula del volumen:

\(V= \pi r^2 \cdot h\)

Área superficial total:

\( \small S = 2 \pi r \cdot h + 2 \cdot \pi r^2 = 2 \pi r(r+h) \)

Área de la superficie lateral:

\(S = 2 \pi r \cdot h \)

Definición:

Un cilindro es una figura geométrica tridimensional con dos bases circulares paralelas y congruentes y una superficie curva que conecta estas bases. Es una de las formas geométricas más comunes y fundamentales.

Características esenciales de un cilindro:

Dos Bases Circulares: Un cilindro tiene dos extremos circulares planos que son idénticos en tamaño y forma. Estas bases son paralelas entre sí.

Superficie Curva: La superficie curva del cilindro conecta las dos bases circulares. Forma una superficie lateral que es suave y no tiene esquinas ni aristas.

Eje: El segmento de línea que conecta los centros de las dos bases circulares se llama eje del cilindro. Es perpendicular a las bases.

Altura: La altura del cilindro es la distancia entre las dos bases circulares a lo largo del eje. Es una medida de qué tan alto es el cilindro.

Radio: El radio es la distancia desde el centro de una de las bases circulares hasta el borde (o perímetro) de esa base. El radio es el mismo para ambas bases.

Prisma ☰

Fórmula del volumen:

\(V= S_\text{base} \cdot h \)

Área superficial total:

\( \small S = 2 S_\text{base} + S_\text{lateral} \)

Área de la superficie lateral:

\(S = P_\text{base} \cdot l \)

Definición:

Un prisma es una figura geométrica tridimensional con dos bases poligonales paralelas y congruentes y caras rectangulares o paralelogramos que conectan los lados correspondientes de las bases. Las características esenciales de un prisma son las siguientes:

Dos Bases Poligonales: Un prisma tiene dos extremos poligonales planos que son idénticos en tamaño y forma. Estas bases son paralelas entre sí.

Caras Rectangulares o Paralelogramos: Las caras del prisma conectan los lados correspondientes de las bases. Estas caras suelen ser rectangulares o paralelogramos.

Aristas: Los segmentos de línea donde se encuentran las caras se llaman las aristas del prisma.

Altura: La altura del prisma es la distancia perpendicular entre las dos bases. Es una medida de qué tan alto es el prisma.

Caras Laterales: Las caras que conectan los lados de las bases se llaman caras laterales. El número de caras laterales es igual al número de lados en las bases poligonales.

Esfera ☰

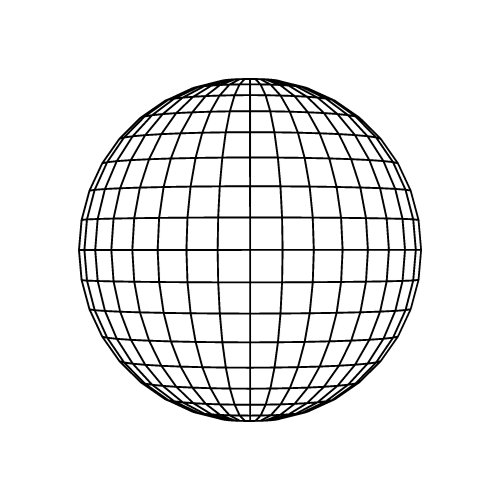
Fórmula del volumen:

\( V = \frac{4}{3} \pi r^3 \)

Área de la superficie:

\( S = 4 \pi r^2 \)

Diámetro:

\( D=2r \)

Definición:

Una esfera es una figura geométrica tridimensional que es perfectamente redonda y simétrica. Se caracteriza por varias características esenciales:

1. Redondez: Una esfera es perfectamente redonda y no tiene aristas ni esquinas. Se define como el conjunto de todos los puntos que están a una distancia fija (el radio) de un punto central (el centro).

2. Centro: El centro de la esfera es un punto ubicado equidistante de todos los puntos en la superficie de la esfera.

3. Superficie: La superficie de una esfera es el conjunto de todos los puntos que están a la misma distancia fija del centro. Forma una superficie continua y curva sin lados planos.

4. Radio: El radio de una esfera es la distancia desde el centro hasta cualquier punto en su superficie. Todos los radios de una esfera tienen la misma longitud.

5. Diámetro: El diámetro es una línea recta que pasa por el centro de la esfera y conecta dos puntos en la superficie de la esfera. Es igual al doble del radio.

Las esferas son una forma geométrica fundamental y se encuentran en varios aspectos de las matemáticas, la ciencia y el mundo físico. Tienen propiedades únicas, como tener el volumen máximo para un área de superficie dada y ser altamente simétricas. Las esferas se encuentran comúnmente en el estudio de la geometría, la astronomía y la ingeniería.