Understanding Curved Solids in Geometry

    Introduction to Curved Solids

    Classification of Curved Solids

    Convex Solids
    Solids where any line segment connecting two points within the solid lies entirely within the solid. Examples include spheres, cones, and cylinders.
    Non-Convex Solids
    Solids where some line segments connecting internal points may lie partially outside the solid. Examples include tori and concave polyhedra.

    Fundamental Theorems

    Pappus's Centroid Theorem
    States that the volume of a solid of revolution equals the product of the generating figure's area and its centroid's rotational path length.
    Cavalieri's Principle
    If two solids have equal heights and equal cross-sectional areas at every height, their volumes are equal.

    Spherical Geometry Properties

    • Parallel Lines: Non-existent in spherical geometry
    • Triangle Angles: Sum exceeds 180 degrees
    • Area Calculation: Proportional to excess angle

    Sphere

    A perfectly symmetrical solid where all surface points are equidistant from the center.

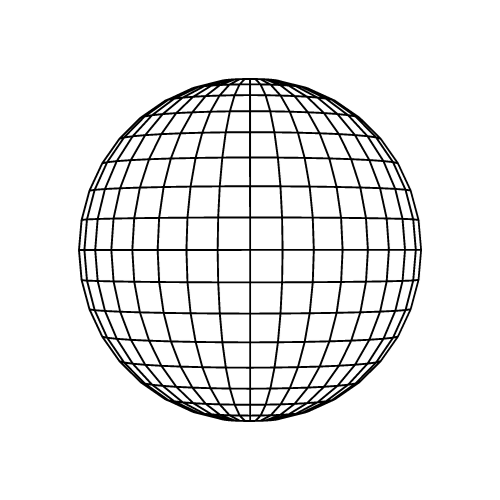
    Sphere
    Sphere

    Key Formulas

    Surface Area
    \(SA = 4\pi r^2\)
    Volume
    \(V = \frac{4}{3}\pi r^3\)
    Diameter
    \(D = 2r\)

    Properties

    • Equal distance from center to all surface points
    • Minimal surface area for given volume
    • Infinite lines of symmetry
    • Optimal volume-to-surface-area ratio

    Real-World Applications

    • Celestial Bodies: Gravitational forces create approximately spherical planets
    • Liquid Droplets: Surface tension forms spherical shapes
    • Pressure Vessels: Spherical tanks for optimal pressure distribution

    Cone

    A solid formed by connecting all points of a flat base to a single vertex point.

    Cone
    Cone

    Essential Formulas

    Lateral Surface Area
    \(S_{LSA} = \pi rl\)
    Total Surface Area
    \(S_{SA} = \pi r(r+l)\)
    Volume
    \(V = \frac{1}{3}\pi r^2h\)
    Slant Height
    \(l = \sqrt{r^2 + h^2}\)

    Cone Frustum

    A cone section formed by parallel cuts to the base.

    \(V = \frac{1}{3}\pi h(R^2 + r^2 + Rr)\)

    Cylinder

    A solid with parallel, congruent bases connected by a curved surface.

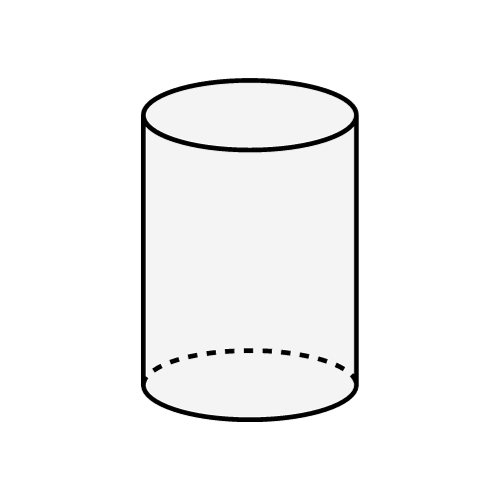
    Cylinder
    Cylinder

    Core Formulas

    Surface Area
    \(SA = 2\pi r^2 + 2\pi rh\)
    Lateral Surface Area
    \(LSA = 2\pi rh\)
    Volume
    \(V = \pi r^2h\)

    Types of Cylinders

    Right Circular Cylinder
    Circular base with perpendicular axis
    Elliptical Cylinder
    Elliptical base with volume formula: \(V = \pi abh\)

    Applications

    • Engineering: Pipes, columns, storage tanks
    • Optics: Cylindrical lenses for astigmatism correction
    • Architecture: Structural supports and decorative elements